一、K近邻算法
K近邻算法简单、直观。首先给出一张图,根据这张图来理解最近邻分类器。
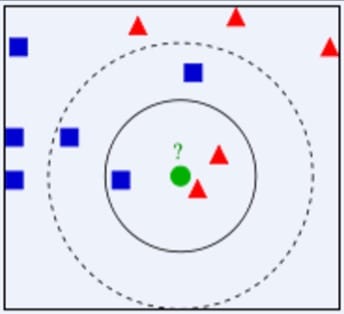
根据上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。也就是说,现在,我们不知道中间那个绿色的数据是从属于哪一类(蓝色小正方形或者红色小三角形),下面,我们就要解决这个问题:给这个绿色的圆分类。
我们常说,物以类聚,人以群分,判别一个人是一个什么样的人,常常可以从他身边的朋友入手,所谓观其友,而识其人。我们不是要判别上图中那个绿色的圆是属于那一类数据么,好说,从他的另据下手。但一次性看多少个邻居呢?从上图中,你还可以看到:
- 如果K=3,绿色圆点最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
- 如果K=5,绿色圆点的最近5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色这个待分类点属于蓝色的正方形一类。
于此,我们看到,KNN算法为给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分为这个类。
K近邻法算法步骤如下:
输入:训练数据集$T={(x_1,y_1),(x_2,y_2),···,(x_N,y_N)}$,其中,$x_i$是实例的特征向量,$y_i$是实例的类别;新实例的特征向量$x$
输出:新实例$x$所属的类别$y$
- 1)根据给定的距离度量,在训练集$T$中找出与$x$最邻近的$k$个点,涵盖这k个点的$x$领域记作$N_k(x)$;
- 2)在$N_k(x)$中根据分类决策规则(如多数表决)决定$x$的类别$y$:
其中$I$为指示函数,即当$y_i=c_i$时为1,否则为0.
二、K近邻模型
2.1 模型
k近邻法中,当训练集、距离度量、K值以及分类决策规则确定后,对于任何一个新的输入实例,它所属的类唯一地确定。这相当于根据上述要素将特征空间划分为一些子空间,确定子空间里的每个点所属的类。
2.2 距离度量
特征空间中两个实例点的距离可以反映出两个实力点之间的相似性程度。K近邻模型的特征空间一般是N维实数向量空间,使用的距离可以是欧式距离,也可以是其他距离。
- 欧氏距离:最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中
曼哈顿距离:我们可以定义曼哈顿距离的正式意义为$L1$距离或城市区块距离,也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投射的距离总和。
通俗来讲,想想你在曼哈顿要从一个十字路口开车到另一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”,此即曼哈顿距离名称的来源,同时,曼哈顿距离也称为城市街区距离。
切比雪夫距离:
闵可夫斯基距离:它不是一种距离,而是一组距离的定义。
当p=1时,即曼哈顿距离
当p=2时,即欧式距离
当$p\rightarrow \infty$,即切比雪夫距离标准化欧氏距离:对样本集先进行标准化$
\hat{x}_i=\frac{x_i-\bar{x}}{s}$经过简单的推导就可以得到来标准化欧氏距离。夹角余弦:几何中夹角余弦可用来衡量两个向量方向的相似度,机器学习中借用这一概念来衡量向量之间的相似度。
2.3 K值的选择
K值得选择会对K近邻法的结果产生重大影响。
如果选择较小的K值,就相当于用较小的领域中的训练实例进行预测,“学习”近似误差会减小,只有与输入实例较近或相似的训练实例才会对预测结果起作用,与此同时带来的问题是“学习”的估计误差会增大,换句话说,K值得减小就意味着整体模型变得复杂,容易发生过拟合(容易受到训练数据的噪声而产生的过拟合的影响)。
如果选择较大的K值,就相当于用较大领域中的训练实例进行预测,其优点是可以减小学习的估计误差,但缺点是学习的近似误差会增大。这时候,与输入实例较远的训练实例也会对预测器作用,使预测发生错误,且K值得增大就意味着整体的模型变得简单。
如果K=N。那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型过于简单,完全忽略训练实例中的大量有用信息,是不可取的(最近邻列表中可能包含远离其近邻的数据点),如下图所示。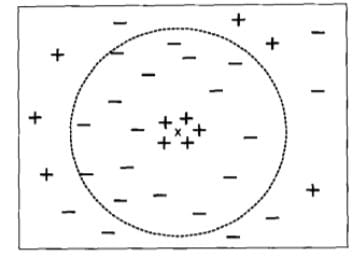
在实际应用中,K值一般取一个比较小的数值。通常采用交叉验证法来选取最优的K值(经验规则:K一般低于训练样本数的平方根)。
2.4 分类决策规则
K近邻法中的分类决策规则往往是多数表决,即由输入实例的K个邻近的训练实例中的多数类决定输入实例的类。
三、K近邻的优缺点
3.1 优点
- 简单、易于理解、易于实现、无需估计参数、无需训练。
- 适合对稀有事件进行分类(如大概流式率很低时,比如0.5%,构造流失预测模型);
- 特别适合多酚类问题,如根据基因特征来判断其功能分类,KNN比SVM的表现要好。
3.2 缺点
- 懒惰算法,对测试样本分类时的计算量大,内存开销大,评分慢。
- 可解释性较差,无法给出决策树那样的规则。
- 当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。
- KNN是一种懒惰算法,平时不好好学习,考试(对测试样本分类)时才临阵磨枪(临时去找K个近邻),懒惰的后果,构造模型很简单,但在测试样本分类地系统开销大,因为要扫描全部训练样本并计算距离。已经有一些方法提高计算的效率,例如压缩训练样本量。
- 决策树和基于规则的分类器都是积极学习
eager learner的例子,因为一旦训练数据可用,它们就开始学习从输入属性到类标号的映射模型。一个相反的策略是推迟对训练数据的建模,直到需要分类测试样例时再进行。采用这种策略的技术被称为消极学习法lazy learner。最近邻分类器就是这样的一种方法。
四、python代码实现
4.1 K-近邻算法简单示例
KNN算法
|
|
4.2 KNN实现手写识别系统
|
|

