一、基本原理
顾名思义,是用随机的方式建立一个森林,森林里面有很多的决策树组成,随机森林的每一棵决策树之间是没有关联的。在得到森林之后,当有一个新的输入样本进入的时候,就让森林中的每一棵决策树分别进行一下判断,看看这个样本应该属于哪一类(对于分类算法),然后看看哪一类被选择最多,就预测这个样本为那一类。
我们可以这样比喻随机森林算法:每一棵决策树就是一个精通于某一个窄领域的专家(因为我们从M个特征中选择m个让每一棵决策树进行学习),这样在随机森林中就有了很多个精通不同领域的专家,对一个新的问题(新的输入数据),可以用不同的角度去看待它,最终由各个专家,投票得到结果。
下图为随机森林算法的示意图: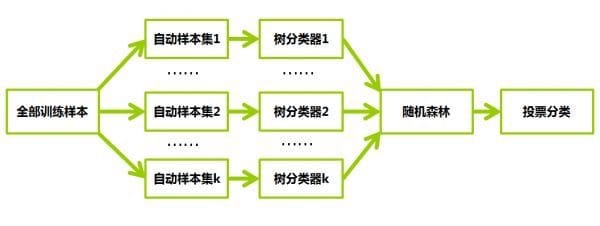
随机森林算法有很多优点:
- 在数据集上表现良好,两个随机性的引入,使得随机森林不容易陷入过拟合
- 在当前的很多数据集上,相对其他算法有着很大的优势,两个随机性的引入,使得随机森林具有很好的抗噪声能力
- 它能够处理很高维度(feature很多)的数据,并且不用做特征选择,对数据集的适应能力强:既能处理离散型数据,也能处理连续型数据,数据集无需规范化
- 可生成一个$Proximities=(p_{ij})$矩阵,用于度量样本之间的相似性: $p_{ij}=a_{ij}/N$,$ a_{ij}$表示样本i和j出现在随机森林中同一个叶子结点的次数,N随机森林中树的颗数
- 在创建随机森林的时候,对generlization error使用的是无偏估计
- 训练速度快,可以得到变量重要性排序(两种:基于OOB误分率的增加量和基于分裂时的GINI下降量
- 在训练过程中,能够检测到feature间的互相影响
- 容易做成并行化方法
- 实现比较简单
二、随机森林的生成
2.1 生成步骤
步骤如下:
- 1)如果训练集大小为$N$,对于每棵树而言,随机且有放回地从训练集中抽取$N$个训练样本(bootstrap抽样方法),作为该树的训练集;每棵树的训练集都是不同的,但里面包含重复的训练样本
- 2)如果每个样本的特征维度为$M$,指定一个常数$m$,且$m$<$M$,随机地从$M$个特征中选取$m$个特征子集,每次树进行分裂时,从这$m$个特征中选择最优的;
- 3)每棵树都尽可能最大程度地生长,并且没有剪枝过程。
2.2 影响分类效果的参数
随机森林的分类效果(即错误率)与以下两个因素有关:
- 1)森林中任意两棵树的相关性:相关性越大,错误率越大
- 2)森林中每棵树的分类能力:每棵树的分类能力越强,整个森林的错误率越低
减小特征选择个数m,树的相关性和分类能力也会相应的降低;增大m,两者也会随之增大。所以关键问题是如何选择最优的m(或者是范围),这也是随机森林唯一的一个参数。
2.3 袋外误差率
如何选择最优的特征个数m,要解决这个问题,我们主要依据计算得到的袋外错误率oob error(out-of-bag error)。
对于一个样本,它在某一次含m个样本的训练集的随机采样中,每次被采集到的概率是$\frac{1}{m}$。不被采集到的概率为$1-\frac{1}{m}$。如果m次采样都没有被采集中的概率是$(1−\frac{1}{m})^m$,当$m→∞$
时,$(1−\frac{1}{m})m→\frac{1}{e}≃0.368$。也就是说,在bagging的每轮随机采样中,训练集中大约有36.8%的数据没有被采样集采集中。对于这部分大约36.8%的没有被采样到的数据,我们常常称之为袋外数据(Out Of Bag, 简称OOB)。这些数据没有参与训练集模型的拟合,因此可以用来检测模型的泛化能力。
袋外错误率(oob error)计算方式如下:
- 1)对每个样本计算它作为oob样本的树对它的分类情况
- 2)以简单多数投票作为该样本的分类结果
- 3)最后用误分个数占样本总数的比率作为随机森林的oob误分率
三、随机采样与完全分裂
在建立每一棵决策树的过程中,有两点需要注意,分别是采样与完全分裂。
3.1 随机采样
首先是两个随机采样的过程,random forest对输入的数据要进行行、列的采样。对于行采样,采用有放回的方式,也就是在采样得到的样本集合中,可能有重复的样本。假设输入样本为N个,那么采样的样本也为N个。这样使得在训练的时候,每一棵树的输入样本都不是全部的样本,使得相对不容易出现over-fitting。然后进行列采样,从M个feature中,选择m个(m << M)。
3.1.1 有放回抽样的解释
如果不是有放回的抽样,那么每棵树的训练样本都是不同的,都是没有交集的,这样每棵树都是”有偏的”,都是绝对”片面的”(当然这样说可能不对),也就是说每棵树训练出来都是有很大的差异的;而随机森林最后分类取决于多棵树(弱分类器)的投票表决,这种表决应该是”求同”,因此使用完全不同的训练集来训练每棵树这样对最终分类结果是没有帮助的,这样无异于是”盲人摸象”。
3.1.2 对Bagging的改进
随机森林对Bagging的改进就在于随机采用的不同,即以下两点:
- 1)Random forest是选与输入样本的数目相同多的次数(可能一个样本会被选取多次,同时也会造成一些样本不会被选取到),而bagging一般选取比输入样本的数目少的样本;
- 2)bagging是用全部特征来得到分类器,而Random forest是需要从全部特征中选取其中的一部分来训练得到分类器; 一般Random forest效果比bagging效果好!
3.2 完全分裂
之后就是对采样之后的数据使用完全分裂的方式建立出决策树,这样决策树的某一个叶子节点要么是无法继续分裂的,要么里面的所有样本的都是指向的同一个分类。一般很多的决策树算法都一个重要的步骤 - 剪枝,但是这里不这样干,由于之前的两个随机采样的过程保证了随机性,所以就算不剪枝,也不会出现over-fitting。 按这种算法得到的随机森林中的每一棵都是很弱的,但是大家组合起来就很厉害了。
四、随机森林的变体
也可以使用SVM、Logistic回归等其他分 类器,习惯上,这些分类器组成的“总分类器”,仍然叫做随机森林。
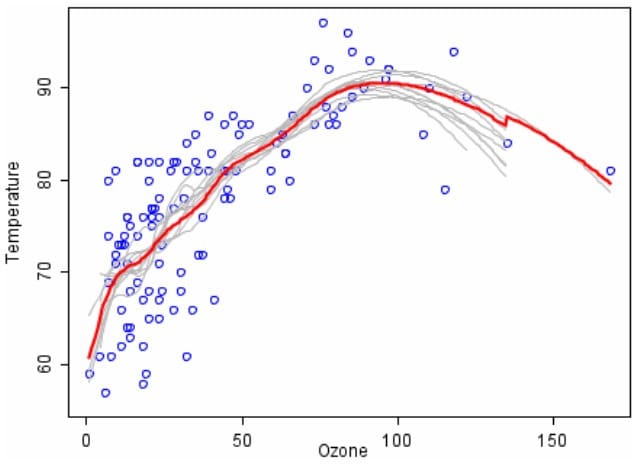
比如回归问题,图中离散点为臭氧(横轴)和温度(纵轴)的关系,试拟合变化曲线,记原始数据为D,长度为N(即图中有N个离散点)
算法过程为:
- 1)做100次bootstrap,每次得到的数据Di,Di的长度为N
- 2)对于每一个Di,使用局部回归(LOESS)拟合一条曲线(图 中灰色线是其中的10条曲线)
- 3)将这些曲线取平均,即得到红色的最终拟合曲线
- 4)显然,红色的曲线更加稳定,并且没有过拟合明显减弱