机器学习算法系列（11）：聚类（2）—Kmeans

三、K-Means算法

3.1 原理

K-Means算法属于基于划分的聚类算法，对N 维欧氏空间中的点进行聚类，是一种最简单的无监督学习方法。它通过迭代来实现，其基本思想是：每次确定K个类别中心，然后将各个结点归属到与之距离最近的中心点所在的Cluster，然后将类别中心更新为属于各Cluster的所有样本的均值，反复迭代，直至类别中心不再发生变化或变化小于某阈值。

3.2 基本假设

K-Means聚类需要对数据进行一个基本假设：对于每一个 cluster ，我们可以选出一个中心点 (center) ，使得该 cluster 中的所有的点到该中心点的距离小于到其他 cluster 的中心的距离。虽然实际情况中得到的数据并不能保证总是满足这样的约束，但这通常已经是我们所能达到的最好的结果，而那些误差通常是固有存在的或者问题本身的不可分性造成的。例如下图所示的两个高斯分布，从两个分布中随机地抽取一些数据点出来，混杂到一起，现在要让你将这些混杂在一起的数据点按照它们被生成的那个分布分开来：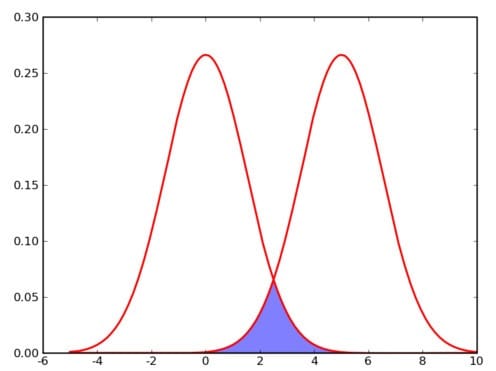
由于这两个分布本身有很大一部分重叠在一起了，例如，对于数据点 2.5 来说，它由两个分布产生的概率都是相等的，你所做的只能是一个猜测；稍微好一点的情况是 2 ，通常我们会将它归类为左边的那个分布，因为概率大一些，然而此时它由右边的分布生成的概率仍然是比较大的，我们仍然有不小的几率会猜错。而整个阴影部分是我们所能达到的最小的猜错的概率，这来自于问题本身的不可分性，无法避免。因此，我们将 k-means 所依赖的这个假设看作是合理的。

3.3 算法步骤

假定输入样本为$S=x_1,x_2,···,x_n$，则算法步骤为：

• 1、选择初始的K个类别中心$\mu_1,\mu_2,···,\mu_k$。这个过程通常是针对具体地问题有一些启发式的选取方法，或者大多数情况下采用随机选取的办法。因为K-Means并不能保证全局最优，而是否能收敛到全局最优解其实和初值的选取有很大的关系，所以有时候我们会多次选取初值跑一个K-Means，并取其中最好的一次结果。
• 2、对于每个样本$x_i$，将其标记为距离类别中心最近的类别，即： $$label_i=arg\underset{1\le j\le k}{\min}||x_i-\mu_j||$$
• 3、将每个类别中心更新为隶属于该类别的所有样本的均值 $$\mu_j=\frac{1}{|c_j|}\sum_{i\in c_j}{x_i}$$
• 4、重复前两步，直到类别中心的变化小于某阈值或者达到最大迭代次数

3.4 理论分析

基于上述的假设，我们导出K-Means所要优化的目标函数：设我们一共有N个数据点需要分为K个Cluster，K-Means需要最小化的损失函数为：

$$J=\frac{1}{2}\sum_{i=1}^N{\sum_{j=1}^K{r_{ij}||x_i-\mu_j||^2}}$$

这个函数，其中$r_{ij}$在数据点$n$被归类到$Cluster(j) $的时候为1，否则为0.直接寻找$r_{ij}$和$\mu_j$来最小化$J$并不容易，不过我们可以通过反复迭代以下两步的方法来进行：

• 1、先固定$\mu_j$，选择最优的$r_{ij}$，很容易看出，只要将数据点归类到离它最近的那个中心就能保证$J$最小，通俗来讲，因为每个样本点都有一个$r_{ij}$，不是0就是1，那么我们要想让$J$最小，就要保证当一个样本的$r_{ij=1}$时，与类别中心距离的平方和达到最小。这一步即
• 2、然后固定$r_{ij}$，再求最优的$\mu_j$。将$J$对$\mu_k$求导并令导数等于零，即令 $$\frac{\partial J}{\partial\mu_j}=\sum_{i=1}^{N_j}{r_{ij}\left(x_i-\mu_j\right)}=0$$ 很容易得到$J$最小的时候$\mu_j$应该满足 $$\mu_j=\frac{\sum_i{r_{ij}x_i}}{\sum_i{r_{ij}}}$$

$\mu_j$的值是所有$Cluster(j)$中的数据点的平均值。由于每一次迭代都是取到$J$的最小值，因此$J$智慧不断地减小或者保持不变，而不会增加，这保证了K-Means最终或到达一个极小值。虽然K-Means并不能保证总是得到全局最优解，但是对于这样的问题，像K-Means这样复杂度的算法，这样的结果已经是很不错了。

3.5 算法演练

下面看一个来自WIKI的实例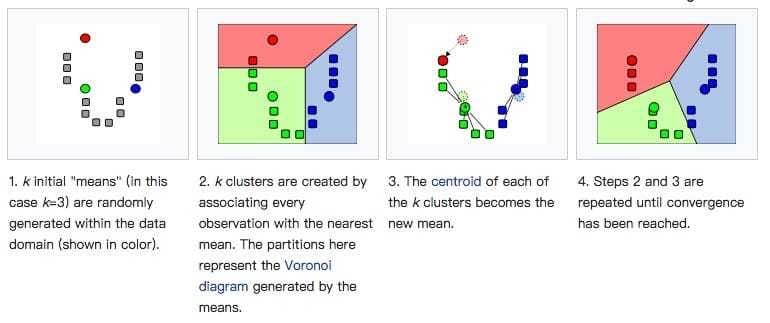

• 1、随机生成三个初始的中心点（这个中心点不一定是样本点），即图中红、绿、蓝三个小圈；
• 2、计算每个样本点与这三个中心店的距离，并将它们归属到离得最近的中心点对应的Cluster。此时图中分成了三个簇，分别是红色、绿色、蓝色部分；
• 3、重新分别计算三个簇中所有样本点的类别中心，指定为新的类别中心。此时红色、绿色、蓝色类的中点都发生了迁移。
• 4、反复迭代第2步和第3步，直至收敛。

3.6 总结

• 优点：
  • 是解决聚类问题的一种经典算法，简单、快速
  • 对处理大数据集，该算法保持可伸缩性和高效率
  • 当簇近似为高斯分布时，它的效果较好
• 缺点
  • 在簇的平均值可被定义的情况下才能使用，可能不适用于某些应用
  • 必须事先给出K，而且对初值敏感，对于不同的初始值，结果可能不同
  • 只能发现球状Cluster，不适合于发现非凸形状的簇或者大小差别很大的簇
  • 对噪声和孤立点数据敏感，如簇中含有异常点，将导致均值偏离严重。因为均值体现的是数据集的整体特征，容易掩盖数据本身的特性。比如数组1，2，3，4，100的均值为22，显然距离“大多数”数据1、2、3、4比较远，如果改成数组的中位数3，在该实例中更为稳妥，这种聚类也叫作K-mediods聚类