机器学习算法系列（12）：SVM（2）—线性支持向量机

当训练数据近似线性可分时，通过软间隔最大化学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机。

二、线性支持向量机与软间隔最大化

2.1 线性支持向量机

通常情况是，训练数据中有一些特异点outlier，将这些特异点除去后，剩下大部分的样本点组成的集合是线性可分的。

线性不可分意味着某些样本点不能满足函数间隔大于等于1的约束条件。为了解决这个问题，可以对每个样本点引进一个松弛变量$\xi \geqslant 0$，使函数间隔加上松弛变量大于等于1.这样，约束条件变成

$$y_i\left( w·x_i+b \right) \geqslant 1-\xi _i$$

同时，对每个松弛变量$\xi \geqslant 0$，支付一个代价$\xi \geqslant 0$。当然，如果我们允许$\xi \geqslant 0$任意大的话，那任意的超平面都是符合条件的了。所以，我们在原来的目标函数后面加上一项，使得这些 $\xi \geqslant 0$的总和也要最小：目标函数由原来的$\frac{1}{2}||w||^2$变成

$$\frac{1}{2}||w||^2+C\sum_{i=1}^N{\xi _i}$$

这里，$C>0$称为惩罚参数，一般事先由应用问题决定，控制目标函数中两项（“寻找 $margin$ 最大的超平面”和“保证数据点偏差量最小”）之间的权重，$C$越大时对误分类的惩罚增大，$C$值小时对误分类的惩罚减小。最小化目标函数包含两层含义：使$\frac{1}{2}||w||^2$尽量小即间隔尽量大，同时使误分类点的个数尽量小，C是调和二者的系数。
则有以下优化问题：

$$\underset{w,b,\xi}{\min}\ \frac{1}{2}||w||^2+C\sum_{i=1}^N{\xi _i}$$ $$s.t.\ \ y_i\left( w·x_i+b \right) \geqslant 1-\xi _i\ ,\ i=1,2,···,N$$ $$\xi _i\geqslant 0,\ i=1,2,···\mathrm{，}N$$

可证明$w$的解是唯一的，但$b$的解不唯一，$b$的解存在于一个区间。

用之前的方法将限制加入到目标函数中，得到如下原始最优化问题的拉格朗日函数：

$$L\left( w,b,\xi ,a,u \right) =\frac{1}{2}||w||^2+C\sum_{i=1}^N{\xi _i-\sum_{i=1}^N{a_i\left( y_i\left( w·x_i+b \right) -1+\xi _i \right) -\sum_{i=1}^N{u_i\xi _i}}}$$

首先求拉格朗日函数针对$w,b,\xi $的极小。

$$\frac{\partial L}{\partial w}=0\Rightarrow w=\sum_{i=1}^N{a_iy_ix_i}$$ $$\frac{\partial L}{\partial b}=0\Rightarrow \sum_{i=1}^N{a_iy_i=0}$$ $$\frac{\partial L}{\partial \xi _i}=0\Rightarrow C-a_i-u_i=0，i=1,2,3···,N$$

将它们代入拉格朗日函数，得到和原来一样的目标函数。

$$\underset{a}{\max}\ \ -\frac{1}{2}\sum_{i=1}^N{\sum_{j=1}^N{a_ia_jy_iy_j\left( x_i·x_j \right) +\sum_{i=1}^N{a_i}}}$$ $$s.t.\ \sum_{i=1}^N{a_iy_i=0}$$ $$C-a_i-u_i=0$$ $$a_i\geqslant 0$$ $$u_i\geqslant 0$$

不过，由于我们得到$C-a_i-u_i=0$，而又有$u_i>0$（作为拉格朗日乘子的条件）,因此有$a_i≤C$,所以整个dual问题现在写作：

$$\underset{a}{\max}\ \ -\frac{1}{2}\sum_{i=1}^N{\sum_{j=1}^N{a_ia_jy_iy_j⟨x_i·x_j ⟩+\sum_{i=1}^N{a_i}}}$$ $$s.t.\ \sum_{i=1}^N{a_iy_i=0}$$ $$0\le a_i\le C\ ,\ \ i=1,2,···,N$$

和之前的结果对比一下，可以看到唯一的区别就是现在拉格朗日乘子$a$多了一个上限$C$。而 Kernel 化的非线性形式也是一样的，只要把$⟨x_i,x_j⟩$ 换成 $κ(x_i,x_j)$ 即可。

构造并求解上述二次规划问题后求得最优解

$$a^*=\left( a_{1}^{*},a_{2}^{*},···,a_{N}^{*} \right) ^T$$

然后计算

$$w^*=\sum_{i=1}^N{a_{i}^{*}y_ix_i}$$

选择$a^$的一个分量$a_i^$适合约束条件$0<a_i<C$,计算

$$b^*=y_j-\sum_{i=1}^N{a_{i}^{*}y_i⟨x_i·x_j ⟩}$$

对任一适合条件都可求得一个$b^*$，但是由于原始问题对$b$的求解并不唯一，所以实际计算时可以取在所有符合条件的样本点上的平均值。

2.2 支持向量

再现性不可分的情况下，将对偶问题的解中对应于$a_i^*>0$的样本点$(x_i,y_i)$的实例$x_i$称为支持向量（软间隔的支持向量）。如图所示，这时的支持向量要比线性可分时的情况复杂一些。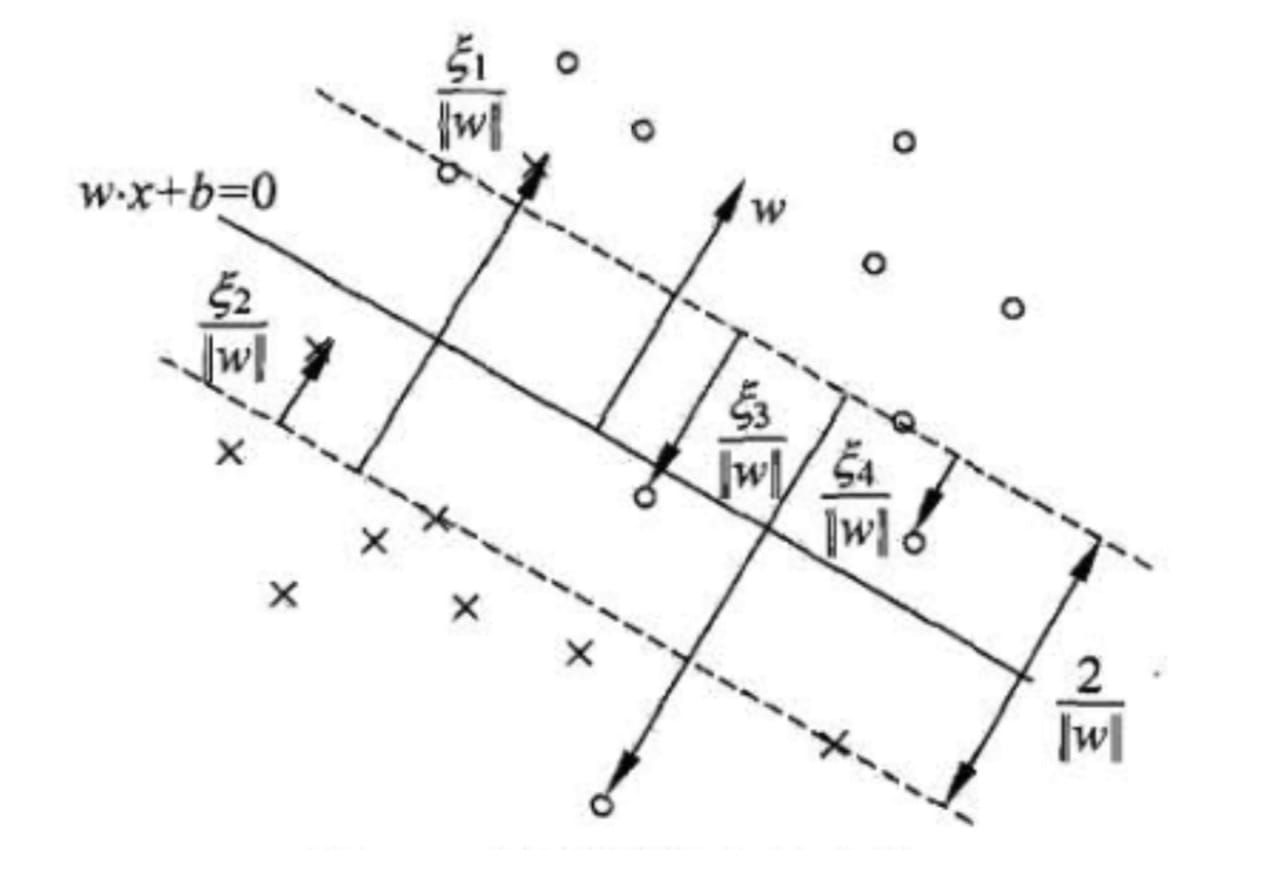

图中，分离超平面由实线表示，间隔边界由虚线表示。正例点由$。$表示，负例点由$×$表示。图中还标出了实例$x_i$到间隔边界的距离$
\frac{\xi _i}{||w||}
$。

软间隔的支持向量$x_i$要么在间隔边界上，要么在间隔边界与分离超平面之间，要么在分离超平面误分类一侧。

若$a_i^*<C$，则$
\xi _i=0
$，支持向量恰好落在间隔边界上；

若$a_i^*=C,0<
\xi _i<1
$，则分类正确，$x_i$在间隔边界与分离超平面之间；

若$a_i^*=C，\xi _i=1$则$x_i$在分隔超平面上；

若$a_i^*=C,\xi _i>1$，则$x_i$位于分离超平面误分一侧。

2.3 Hinge损失函数

线性支持向量机学习除了原始最优化问题，还有另外一种解释，就是最优化以下目标函数：

$$\sum_i^{N}[1-y_i(w·x_i+b)]_++\lambda||w||^2$$

目标函数的第一项是经验损失或经验风险，函数

$$L(y·(w·x+b))=[1-y(w·x+b)]_+$$

称为合页损失函数（hinge loss function）。下标”+”表示以下取正值的函数：

$$\left[z\right]_+=\left\{\begin{array}{l} z\ ,\ z>0\\ 0\ ,\ z\le 0\\ \end{array}\right.$$

这就是说，当样本点$(x_i,y_i)$被正确分类且函数间隔（确信度）$y_i(w·x_i+b)$大于1时，损失是0，否则损失是$1-y_i(w·x_i+b)$。目标函数的第二项是系数为$\lambda$的$w$的$L_2$范数，是正则化项。

接下来证明线性支持向量机原始最优化问题：

$$\underset{w,b,\xi}{\min}\ \frac{1}{2}||w||^2+C\sum_{i=1}^N{\xi _i}$$ $$s.t.\ \ y_i\left( w·x_i+b \right) \geqslant 1-\xi _i\ ,\ i=1,2,···,N$$ $$\xi _i\geqslant 0,\ i=1,2,···\mathrm{，}N$$

等价于最优化问题

$$\underset{w,b}{min }\sum_i^{N}[1-y_i(w·x_i+b)]_++\lambda||w||^2$$

先令$[1-y_i(w·x_i+b)]_+=\xi_i$，则$\xi_i≥0$，第二个约束条件成立；由$[1-y_i(w·x_i+b)]_+=\xi_i$，当$1-y_i(w·x_i+b)>0$时，有$y_i(w·x_i+b)=1-\xi_i$;当$1-y_i(w·x_i+b)≤0$时，$\xi_i=0$，有$y_i(w·x_i+b)≥1-\xi_i$，所以第一个约束条件成立。所以两个约束条件都满足，最优化问题可以写作

$$\underset{w,b}{min}\sum_{i=1}^N\xi_i+\lambda||w||^2$$

若取$\lambda =\frac{1}{2C}$则$\underset{w,b}{min} \frac{1}{C}(\frac{1}{2} ||w||^2+C\sum_{i=1}^N \xi_i)$与原始最优化问题等价。

合页损失函数图像如图所示，横轴是函数间隔$y(w·x+b)$，纵轴是损失。由于函数形状像一个合页，故名合页损失函数。

图中还画出了0-1损失函数，可以认为它是一个二类分类问题的真正的损失函数，而合页损失函数是0-1损失函数的上界。由于0-1损失函数不是连续可导的，直接优化其构成的目标函数比较困难，可以认为线性支持向量机是优化由0-1损失函数的上界（合页损失函数）构成的目标函数。这时的上界损失函数又称为代理损失函数（surrogate function）。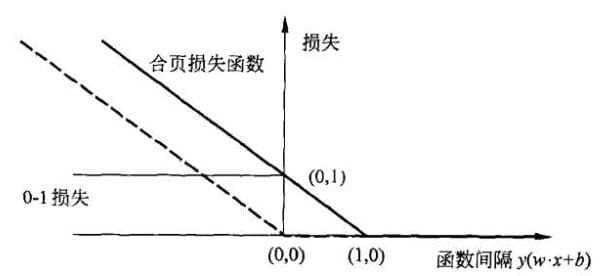

图中虚线显示的是感知机的损失函数$[-y_i(w·x_i+b)]_+$。这时当样本点$(x_i,y_i)$被正确分类时，损失是0，否则损失是$-y_i(w·x_i+b)$，相比之下，合页损失函数不仅要分类正确，而且确信度足够高时损失才是0，也就是说，合页损失函数对学习有更高的要求