机器学习算法系列（13）：推荐系统（3）—矩阵分解技术

随着Netflix Prize推荐比赛的成功举办，近年来隐语义模型（Latent Factor MOdel，LFM）受到越来越多的关注。隐语义模型最早在文本挖掘领域被提出，用于寻找文本的隐含语义，相关的模型常见的有潜在语义分析（Latent Semantic Analysis,LSA）、LDA（Latent Dirichlet Allocation）的主题模型（Topic Model）、矩阵分解（Matrix Factorization）等等。

其中矩阵分解技术是实现隐语义模型使用最广泛的一种方法，其思想也正来源于此，注明的推荐领域大神Yehuda Koren更是凭借矩阵分解模型勇夺Netflix Prize推荐比赛冠军，以矩阵分解为基础，Yehuda Koren在数据挖掘和机器学习相关的国际顶级会议（SIGIR,SIGKDD,RecSys等）发表了很多文章，将矩阵分解模型的优势发挥得淋漓尽致。实验结果表明，在个性化推荐中使用矩阵分解模型要明显优于传统的基于邻域的协同过滤(又称基于领域的协同过滤)方法，如UserCF、ItemCF等，这也使得矩阵分解成为了目前个性化推荐研究领域中的主流模型。

需要说明的是，协同过滤方法分为两大类，一类为上述基于领域的方法，第二类为基于模型的方法，即隐语义模型，矩阵分解模型是隐语义模型最为成功的一种实现，不作特别说明的情况下，本文将隐语义模型和矩阵分解看做同一概念，User-Item矩阵和User-Item评分矩阵为同一概念。

一、传统的SVD算法

说到矩阵分解，我们首先想到的就是奇异值分解SVD。我们可以把User-Item评分矩阵M进行SVD分解，并通过选择部分较大的一些奇异值来同时进行降维，也就是说矩阵M此时分解为：

$$M_{m\times n}=U_{m\times k}\Sigma_{k\times k}V^T_{k\times n}$$

其中k是矩阵MM中较大的部分奇异值的个数，一般会远远的小于用户数和物品数。

如果我们要预测第i个用户对第j个物品的评分$m_{ij}$,则只需要计算$u^T_iΣv_j$即可。通过这种方法，我们可以将评分表里面所有没有评分的位置得到一个预测评分，通过找到最高的若干个评分对应的物品推荐给用户。

可以看出这种方法简单直接，似乎很有吸引力。但是有一个很大的问题我们忽略了，就是SVD分解要求矩阵是稠密的，也就是说矩阵的所有位置不能有空白。有空白时我们的MM是没法直接去SVD分解的。大家会说，如果这个矩阵是稠密的，那不就是说我们都已经找到所有用户物品的评分了嘛，那还要SVD干嘛! 的确，这是一个问题，传统SVD采用的方法是对评分矩阵中的缺失值进行简单的补全，比如用全局平均值或者用用户物品平均值补全，得到补全后的矩阵。接着可以用SVD分解并降维。但填充本身会造成很多问题，其一，填充大大增加了数据量，增加了算法复杂度。其二，简单粗暴的数据填充很容易造成数据失真。

虽然有了上面的补全策略，我们的传统SVD在推荐算法上还是较难使用。因为我们的用户数和物品一般都是超级大，随便就成千上万了。这么大一个矩阵做SVD分解是非常耗时的。那么有没有简化版的矩阵分解可以用呢？我们下面来看看实际可以用于推荐系统的矩阵分解。

二、Funk-SVD算法

2.1 基本思想

Funk-SVD的核心思想认为用户的兴趣只受少数几个因素的影响，因此将稀疏且高维的User-Item评分矩阵分解为两个低维矩阵，即通过User、Item评分信息来学习到的用户特征矩阵P和物品特征矩阵Q，通过重构的低维矩阵预测用户对产品的评分。由于用户和物品的特征向量维度比较低，因而可以通过梯度下降(Gradient Descend)的方法高效地求解，分解示意图如下所示。

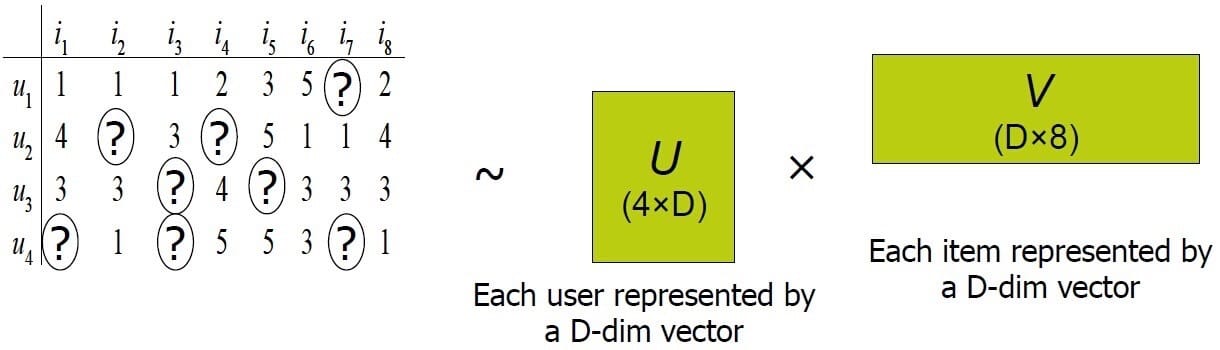
2.2 Funk-SVD

Simon Funk在博客上公开发表了一个只考虑已有评分记录的矩阵分解方法，称为Funk-SCD，也就是被Yehuda Koren称为隐语义模型的矩阵分解方法。

它的出发点为，既然将一个矩阵做SVD分解成3个矩阵很耗时，同时还面临稀疏的问题，那么我们能不能避开稀疏问题，同时只分解成两个矩阵呢？也就是说，现在期望我们的矩阵M这样进行分解：

$$M_{m\times n}=P^T_{m\times k}Q_{k\times n}$$

我们知道SVD分解已经很成熟了，但是Funk-SVD如何将矩阵M分解成为P和Q呢？这里采用了线性回归的思想。我们的目标是让用户的评分和用矩阵乘积得到的评分残差尽可能的小，也就是说，可以用均方差作为损失函数，来寻找最终的P和Q。

对于某一个用户评分$m_{ij}$如果用Funk-SVD进行矩阵分解，则对应的表示为$q_j^Tp_i$，采用均方差作为损失函数，则我们期望$(m_{ij}-q_j^Tp_i)^2$尽可能的小，如果考虑所有的物品和样本的组合，则我们期望最小化下式：

$$\sum_{i，j}(m_{ij}-q^T_jp_i)^2$$

只要我们能够最小化上面的式子，并求出极值所对应的$p_i,q_j$，则我们最终可以得到矩阵P和Q，那么对于任意矩阵M任意一个空白评分的位置，我们可以通过$q_j^Tp_i$计算预测评分，很漂亮的方法！

当然，在实际应用中，为了防止过拟合，会加入一个$L_2$的正则化项，因此正是的Funk-SVD的优化目标函数$J(p,q)$是这样的：

$$arg \underset {p_jq_j}{min}\sum_{(i,j)\in K}(m_{ij}-q_j^Tp_i)^2+\lambda (||p_i||^2_2+||q_j||^2_2)$$

其中$K$为已有评分记录的$(i,j)$对集合，$m_{ij}$为用户$i$对物品$$j$的真实评分，$\lambda$是正则化系数，需要调参。假设输入评分矩阵为M，它是$M \times N$维矩阵，通过直接优化以上损失函数得到用户特征矩阵$P(M\times N)$和物品特征矩阵$Q(K\times N)$,其中$K<<M，N$。对于这个优化问题，一般通过梯度下降法来进行优化得到结果。

将上式分别对$p_i,q_j$求导我们得到：

$$\frac{∂J}{∂p_i}=-2(m_{ij}-q_j^Tp_i)q_j+2\lambda p_i$$$$\frac{∂J}{∂q_j}=-2(m_{ij}-q_j^Tp_i)p_i+2\lambda q_j$$

在梯度下降法迭代时，$p_i,q_j$的迭代公式为：

$$p_i=p_i=\alpha [(m_{ij}-q_j^Tp_i)q_j-\lambda p_i]$$ $$q_j=q_j+\alpha [(m_{ij}-q_j^Tp_i)p_i-\lambda q_j ]$$

通过迭代我们最终可以得到P和Q，进而用于推荐。Funk-SVD算法虽然思想很简单，但在实际应用中效果非常好，这真是验证了大道至简。

三、Bias-SVD

在Funk-SVD算法火爆之后，出现了很多Funk-SVD的改进版算法。其中Bias算是改进的比较成功的一种算法。

Funk-SVD方法通过学习用户和物品的特征向量进行预测，即用户和物品的交互信息。用户的特征向量代表了用户的兴趣，物品的特征向量代表了物品的特点，且每一个维度相互对应，两个向量的内积表示用户对该物品的喜好程度。但是我们观测到的评分数据大部分都是都是和用户或物品无关的因素产生的效果，即有很大一部分因素是和用户对物品的喜好无关而只取决于用户或物品本身特性的。例如，对于乐观的用户来说，它的评分行为普遍偏高，而对批判性用户来说，他的评分记录普遍偏低，即使他们对同一物品的评分相同，但是他们对该物品的喜好程度却并不一样。同理，对物品来说，以电影为例，受大众欢迎的电影得到的评分普遍偏高，而一些烂片的评分普遍偏低，这些因素都是独立于用户或产品的因素，而和用户对产品的的喜好无关。

我们把这些独立于用户或独立于物品的因素称为偏置(Bias)部分，将用户和物品的交互即用户对物品的喜好部分称为个性化部分。事实上，在矩阵分解模型中偏好部分对提高评分预测准确率起的作用要大大高于个性化部分所起的作用，以Netflix Prize推荐比赛数据集为例为例，Yehuda Koren仅使用偏置部分可以将评分误差降低32%，而加入个性化部分能降低42%，也就是说只有10%是个性化部分起到的作用，这也充分说明了偏置部分所起的重要性，剩下的58%的误差Yehuda Koren将称之为模型不可解释部分，包括数据噪音等因素。

偏置部分主要由三个子部分组成，分别是

• 训练集中所有评分记录的全局平均数$\mu$，表示了训练数据的总体评分情况，对于固定的数据集，它是一个常数。
• 用户偏置$b_i$，独立于物品特征的因素，表示某一特定用户的打分习惯。例如，对于批判性用户对于自己的评分比较苛刻，倾向于打低分；而乐观型用户则打分比较保守，总体打分要偏高。
• 物品偏置$b_j$，特立于用户兴趣的因素，表示某一特定物品得到的打分情况。以电影为例，好片获得的总体评分偏高，而烂片获得的评分普遍偏低，物品偏置捕获的就是这样的特征。

则偏置部分表示为

$$b_{ij}=\mu+b_i+b_j$$

则加入了偏置项以后的优化目标函数$J(p,q)$是这样

$$arg \underset {p_jq_j}{min}\sum_{(i,j)\in K}(m_{ij}-\mu-b_i-b_j-q_j^Tp_i)^2+\lambda (||p_i||^2_2+||q_j||^2_2+||b_i||_2^2+||b_j||_2^2)$$

这个优化目标也可以采用梯度下降法求解。和Funk-SVD不同的是，此时我们多了两个偏置项$b_i,b_j$,$p_i,p_j$的迭代公式和$Funk-SVD$类似，只是每一步的梯度导数稍有不同而已。而$b_i,b_j$一般可以初始设置为0向量，然后参与迭代。

$$b_i=b_i+α(m_{ij}−μ−b_i−b_j−q^T_jp_i−λb_i)$$ $$b_j=b_j+α(m_{ij}−μ−b_i−b_j−q^T_jp_i−λb_j)$$

通过迭代我们最终可以得到$P$和$Q$，进而用于推荐。Bias-SVD增加了一些额外因素的考虑，因此在某些场景会比FunkSVD表现好。

四、SVD++

SVD++算法在Bias-SVD算法上进一步做了增强，这里它增加考虑用户的隐式反馈。

对于某一个用户$i$，它提供了隐式反馈的物品集合定义为$N(i)$，这个用户对某个物品$j$对应的隐式反馈修正的评分值为$c_{ij}$，那么该用户所有的评分修正值为$\sum_{s\in N(i)} c_{sj}$，一般我们将它们表示为用$q_j^Ty_s$形式，则加入了隐式反馈以后的优化目标函数$J(p,q)$是这样的：

$$arg \underset {p_jq_j}{min}\sum_{(i,j)\in K}(m_{ij}-\mu-b_i-b_j-q_j^Tp_i-q_j^T|N(i)|^{-1/2}\Sigma_{s\in N(i)} y_s)^2+\lambda (||p_i||^2_2+||q_j||^2_2+||b_i||_2^2+||b_j||_2^2+\Sigma_{s\in N(i)}||y_s||^2)$$

其中，引入$|N(i)|^{-1/2}$是为了消除不同$|N(i)|$个数引起的差异。如果需要考虑用户的隐式反馈时，使用SVD++是个不错的选择。

五、矩阵分解的优缺点

矩阵分解方法将高维User-Item评分矩阵映射为两个低维用户和物品矩阵，解决了数据稀疏性问题。

使用矩阵分解具有以下优点：

• 比较容易编程实现，随机梯度下降方法依次迭代即可训练出模型。比较低的时间和空间复杂度，高维矩阵映射为两个低维矩阵节省了存储空间，训练过程比较费时，但是可以离线完成；评分预测一般在线计算，直接使用离线训练得到的参数，可以实时推荐。
• 预测的精度比较高，预测准确率要高于基于领域的协同过滤以及内容过滤等方法。
• 非常好的扩展性，很方便在用户特征向量和物品特征向量中添加其它因素，例如添加隐性反馈因素的SVD++，此方法的详细实现参见文献《Koren Y. Factorization meets the neighborhood: a multifaceted collaborative filtering model》；添加时间动态time SVD++，此方法将偏置部分和用户兴趣都表示成一个关于时间的函数，可以很好的捕捉到用户的兴趣漂移，欲知详细实现请阅读文献《Koren Y. Collaborative filtering with temporal dynamics》。

矩阵分解的不足主要有：

• 模型训练比较费时。
• 推荐结果不具有很好的可解释性，分解出来的用户和物品矩阵的每个维度* 无法和现实生活中的概念来解释，无法用现实概念给每个维度命名，只能理解为潜在语义空间。