一、关联分析
1.1 引言
在数据挖掘与机器学习中，关联规则（Association Rules）是一种较为常用的无监督学习算法，与分类、聚类等算法不同的是，这一类算法的主要目的在于发掘数据内在结构特征之间的关联性。
简单一点来说，就是在大规模的数据集中寻找一些有意义有价值的关系。有了这些关系，一方面，可以帮助我们拓宽对数据及其特征的理解；另一方面，则可以实现推荐系统的构建与应用（例如购物篮分析等）。
在对关联规则有了基本的认识后，我们对其进行进一步的细分，以日常生活中的关联性举例，在逛超市的顾客中，购买面包的人很大程度上会购买牛奶，这一类的关联性被称为简单关联规则；再例如，购买汽车遮阳板的很多顾客会在近期内购买零度玻璃水，这样的事例不仅反映了事物间的关联关系，而且还具有时间上的先后顺序，因此这一类的关联性被称为序列关联规则。
广义上的关联规则包含了简单关联和序列关联，接下来我们分别对这两块知识进行深入学习。
1.2 简单关联规则初探
首先我们需要明确关联分析中的一些基本概念：
- 事务：指关联分析中的分析对象，我们可以把它理解成为一种宽泛行为（例如顾客的一次超市购买行为，电脑的使用者的一次网页浏览行为等都可以称之为事务），由事务标识（TID）与项目集合组成。
项集：即事务中的一组项目的集合，单个的项目可以是一种商品、一个网页链接等。假设$X$为项集，$I$为项目全体且$I=\{i_1,i_2,···,i_n\}$，那么项集$X\subseteq I$。进一步的，如果$X$中包含$p$个项目，则称该项集为$p-$项集。
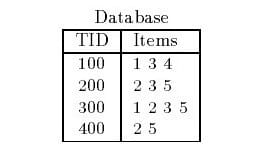以上图为例，这里包含了4个事务，$I$包含了5个项目。对于第一个事务而言，由于$X$包含了三个项目，所以该$X$是一个$3-$项集。
明确了基本概念后，接下来学习关联规则的一般表现形式其中：
$X$和$Y$分别为规则的前项和后项，前项为项目或项集，后项表示某种结论或事实。
- $S=s\%$表示规则支持度为$s\%$，$C=c\%$表示规则置信度为$c\%$
到这里大家可能会疑惑，直接得到关联规则不就可以了吗？为什么要在结论中加入支持度和置信度呢？这就涉及到关联分析中非常重要的一块内容——有效性的判别
1.3 简单关联规则的有效性
实际上，在数据中使用关联分析进行探索时，我们可以找出很多关联规则，但并非所有的关联规则都是有效的，有的可能令人信服的程度并不高，也有的可能适用范围很有限，带有这些特征的所谓“关联规则”，我们则称之为不具有“有效性”。
判断一条关联规则是否有效，需要用到以下两大测度指标，即规则置信度与规则支持度。
1.规则置信度（Confidence）
置信度是对简单关联规则准确度的测量，定义为包含项目$A$的事务中同时也包含项目$B$的概率，数学表述为：
置信度的本质就是我们所学过的条件概率，置信度越高，则说明$A$出现则$B$出现的可能性也就越高。假设在电脑$\rightarrow$杀毒软件的关联规则中，置信度$C=60\%$，表示购买电脑的顾客中有$60\%$的顾客也购买了杀毒软件。
2.规则支持度（Support）
支持度测量了简单关联规则应用的普适性，定义为项目$A$与项目$B$同时出现的概率，数学表述为：
假设某天共有100个顾客到商场购买物品，其中有10个顾客同时购买了电脑和杀毒软件，那么上述关联规则的支持度就为10%，同样，支持度越高，表明某一关联规则的适用性就越大。
一个有效的简单关联规则，势必同时具有较高的置信度与支持度。因为，如果支持度较高而置信度较低，则证明规则的可信度差；而相反，如果支持度较低而置信度较高，则说明规则的应用范围较小。
举例来说，假设在1000个顾客购买行为的事务中，只有一个顾客购买了烧烤炉，同时也只有他购买了碳，虽然规则“烧烤炉$\rightarrow$碳”的置信度很高，为100%，但支持度仅有0.1%，说明这条规则缺乏普遍性，应用价值不高。
所以一个有效的关联规则，必须具有较高的置信度与支持度，那么在实际应用中，我们就需要给定最小的置信度$C_{min}$与支持度$S_{min}$，只要同时大于$C_{min}$和$S_{min}$的规则，我们才可以将其定义为是“有效”的。
1.4 简单关联规则的实用性
在对关联规则的有效性有一个基本的掌握后，我们在此基础上进行进一步的探讨——关联规则的实用性。
关联规则的实用性主要体现在以下两个方面：
- 1）是否具有实际意义。例如“怀孕$\rightarrow $女性”的关联规则就没有实用价值。
- 2）是否具有指导意义，即帮助我们在现有的基础上做出有价值的优化。
对第二点进一步展开说明，假设“牛奶$\rightarrow $男性顾客（$S=40\%，C=40\%$）”在$C_{min}$和$S_{min}$均为20%时是一条有效规则时，如果进一步计算发现顾客中男性的比例也为40%，也就是说购买牛奶的男性顾客等于所有顾客中的男性比例，那么这条规则就是一条前后项无关的随机性关联，因此它就没有有意义的指导信息，不具有实用性。
如何衡量关联规则具有实用性呢？这里我们就需要借助规则的提升度了。
规则提升度（Lift）：置信度与后项支持度之比，数学表述为：
提升度反映了项目$A$的出现对项目$B$出现的影响程度。从统计角度来看，如果$A$的出现对项$B$的出现没有影响，即$A$与$B$相互独立的化，$P(AB)=P(A)P(B)$，此时规则提升度为1。所以，具有实用性的关联规则应该是提升度大于1的规则，即$A$的出现对$B$的出现有促进作用。同样，提升度越大，证明规则实用性越强。
这样我们就阐述清楚了关联规则的一些基本假定与判别标准，当数据集较小时，关联规则的使用较为简单，但是如果数据集很大的话，如何在这海量的数据中快速找出关联规则呢？这就引出了进一步要叙述的内容——简单关联规则下的$Apriori$算法。
二、Apriori算法
2.1 简介
在数据量庞大的前提下，由于简单搜索可能产生大量无效的关联规则，并导致计算效率底下。出于克服这些弊端的目的，Apriori算法应运而生，该算法自1996年提出后，经过不断地完善和发展，已成为简单关联分析中的核心算法。
2.2 频繁项集的相关定义
频繁项集很好理解，他是指大于等于最小支持度$S_{min}$的项集。其中，若频繁项集中包含一个项目，则成为频繁$1-$项集，记为$L_1$；若包含$k$个项目，则成为频繁$k-$项集，记为$L_k$。
频繁项集具有以下两个性质，这俩条性质将应用于我们后面频繁项集及其关联规则的寻找中：
- 1）频繁项集的子集必为频繁项集（假设项集$\{A,C\}$是频繁项集，那么$\{A\}$和$\{C\}$也为频繁项集）
- 2）非频繁集的超集一定也是非频繁的（假设项集$\{D\}$不是频繁项集，那么$\{A,D\}$和$\{C,D\}$也不是频繁项集）
进一步，当某一个$L_k$的所有超集都是频繁项集时，我们就可以称此$L_k$为最大频繁$k-$项集，确定它的目的就在于使之后的到的关联规则具有较高的普适性。
2.3 寻找频繁项集
对频繁项集的寻找，是Apriori算法提高寻找规则效率的关键。它采用迭代的方式逐层寻找下层的超集，并在超集中发现频繁项集。经过层层迭代，直到最顶层得到最大频繁项集为止。在每一轮的迭代中都包含以下两个步骤：
- 1）产生候选集$C_k$，它是有可能成为频繁项集的项目集合；
- 2）修剪候选集$C_k$，即基于$C_k$计算相应的支持度，并依据最小支持度$S_{min}$对候选集$C_k$进行删减，得到新的候选集$C_{k+1}$，如此循环迭代，直到无法产生候选项集为止，这样最后一轮所得到的频繁项集就是Apriori所要求的最大频繁项集。
接下来我们以一个下例子帮助理解：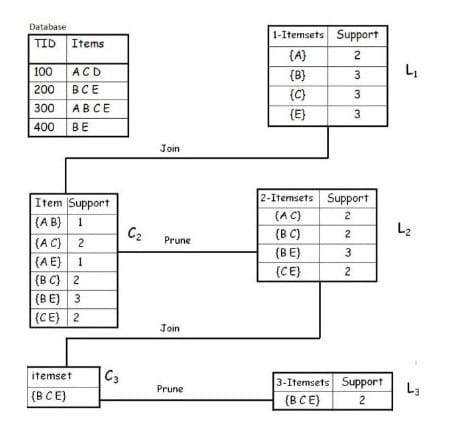
假设我们指定的最小支持阀度为0.5（计数≥2）
- 在第一轮迭代过程中，由于$D$的支持度小于0.5（只有0.25），所以没有进入频繁项集，其余均进入频繁项集，定义为$L_1$。
- 在第二轮迭代中，候选集$C_2$是$L_1$中所有项目的组合，计算各项目支持度，淘汰$\{A,B\}$和$\{A,E\}$，其余进入频繁项集，定义为$L_2$。
- 在第三轮迭代中，只有$\{B,C,E\}$进入候选集$C_3$，而其余都没有进入，之所以会这样，是因为这里使用到了前面所提到的频繁项集的第二个性质：非频繁项集的超集一定也是非频繁的。所以，包含$\{A,B\}$与$\{A,E\}$的超集是不可能成为频繁项集的。
由于$L_3$不能继续构成候选集$C_4$，所以迭代结束，得到的最大频繁项集为$L_3\{B,C,E\}$。
2.4 在最大频繁项集的基础上产生简单关联规则
得到最大频繁项集并不是最终的目的。之前在判断关联规则的有效性时，我们学习了置信度与支持度两个指标。其中，支持度已经在寻找最大频繁项集的过程中发挥了作用，那么，在接下来关联规则的产生上，就轮到置信度大显身手了。
首先，每个频繁项集都需要计算所有非空子集$L^*$的置信度，公式为
如果所求得的$C_{L’\rightarrow\left\{L-L’\right\}}$大于我们自行指定的$C_{min}$，则生成相应的关联规则${L’\rightarrow\left\{L-L’\right\}}$
在上面的例子中，$L_3{\{B,C,E\}}$的非空子集就包括$\{B\}$，$\{C\}$，$\{E\}$，$\{B,C\}$，$\{B,E\}$，$\{C,E\}$，举例来说，根据公式可计算得到
其余置信度依次为：$C_{B\rightarrow\left\{C,E\right\}}=66.7\%$，$C_{E\rightarrow\left\{B,C\right\}}=66.7\%$，$C_{\left\{B,C\right\}\rightarrow E}=100\%$，$C_{\left\{B,E\right\}\rightarrow C}=66.7\%$，$C_{\left\{C,E\right\}\rightarrow B}=100\%$
如果我么设定$C_{min}=80\%$的话，只有$C_{\left\{C,E\right\}\rightarrow B}$和$C_{\left\{B,C\right\}\rightarrow E}$可以入围，如果设定为$50\%$，那么六条规则就都是有效规则了。置信度的选取和支持度一样，只有结合具体应用情况，算法才能给到我们切合实际的结论。
