Free Will

深度学习系列（2）：神经网络MNIST实战

发表于 | 分类于 |

近似非常不错

一、数据集与任务介绍

MNIST数据集是一个基本的手写字体识别数据集，该数据原本是包含60000个训练图像和10000个测试图像，但这里我们事先对数据进行了划分，从训练样本中抽取10000个数据作为验证集，所以处理后的数据集包含50000个训练样本（training data）、10000个验证样本（validation data）10000个测试样本（test data），都是28乘以28的分辨率。

我们可以先将数据集从GitHub上Clone下来：

1
➜  fig git:(master) ✗ git clone https://github.com/lisa-lab/DeepLearningTutorials

可以从这个链接了解对该数据集的加载和处理。

这里任务就是构建神经网络来实现对于MNIST数据集的手写字体识别分类。从任务和输入就能够得到大概的网络结构：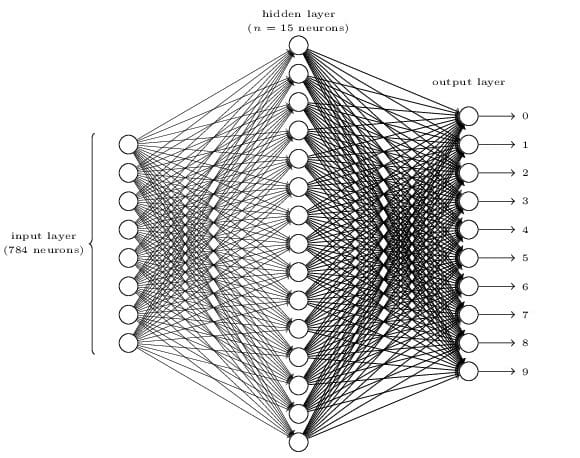

损失函数为平方误差损失函数，激活函数为sigmoid函数。

二、读取数据

读取数据由mnist_loader.py这个文件实现。
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# -*- coding: utf-8 -*-
"""
mnist_loader
~~~~~~~~~~~~
A library to load the MNIST image data.  For details of the data
structures that are returned, see the doc strings for ``load_data``
and ``load_data_wrapper``.  In practice, ``load_data_wrapper`` is the
function usually called by our neural network code.
"""
#### Libraries
# Standard library
import cPickle
import gzip
# Third-party libraries
import numpy as np
#从数据集中载入数据
def load_data():
    f = gzip.open('../data/mnist.pkl.gz', 'rb')
    training_data, validation_data, test_data = cPickle.load(f)
    f.close()
    return (training_data, validation_data, test_data)
#改变数据集的格式
def load_data_wrapper():
    tr_d, va_d, te_d = load_data()
    #训练集
    training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
    training_results = [vectorized_result(y) for y in tr_d[1]]
    training_data = zip(training_inputs, training_results)
    #验证集
    validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
    validation_data = zip(validation_inputs, va_d[1])
    #测试集~~~~
    test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
    test_data = zip(test_inputs, te_d[1])
    return (training_data, validation_data, test_data)
def vectorized_result(j):
    """Return a 10-dimensional unit vector with a 1.0 in the jth
    position and zeroes elsewhere.  This is used to convert a digit
    (0...9) into a corresponding desired output from the neural
    network."""
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e

2.1 load_data函数

1
2
3
4
5
def load_data():
    f = gzip.open('../data/mnist.pkl.gz', 'rb')
    training_data, validation_data, test_data = cPickle.load(f)
    f.close()
    return (training_data, validation_data, test_data)

load_data()函数的主要作用就是解压数据集，然后从数据集中把数据取出来。取出来之后的几个变量代表的数据的格式分别如下：2019-05-16-083034.jpg

training_data：是一个由两个元素构成的元组。其中一个元素是测试图片集合，是一个50000✖️784的numpy ndarray（其中50000行就是样本个数，784列就是一个维度，即一个像素）；第二个元素就是一个测试图片的标签集，是一个50000✖️1的Numpy ndarray，其中指明了每一个样本是什么数字，通俗来说就是这个样子：
validation_data 和 test_data 的结构和上面的training_data是一样的，只是数量不一样，这两个是10000行。

2.2 load_data_wrapper()函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def load_data_wrapper():
    tr_d, va_d, te_d = load_data()
    #训练集
    training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
    training_results = [vectorized_result(y) for y in tr_d[1]]
    training_data = zip(training_inputs, training_results)
    #验证集
    validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
    validation_data = zip(validation_inputs, va_d[1])
    #测试集~~~~
    test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
    test_data = zip(test_inputs, te_d[1])
    return (training_data, validation_data, test_data)

之前的load_data返回的格式虽然很漂亮，但是并不是非常适合我们这里计划的神经网络的结构，因此我们在load_data的基础上使用load_data_wrapper（）函数来进行一点点适当的数据集变换，使得数据集更加适合我们的神经网络训练。

以训练集的变换为例。对于training_inputs来说，就是把之前的返回的training_data[0]，即第一个元素的所有样例都放到一个列表中，简单的来说如下所示：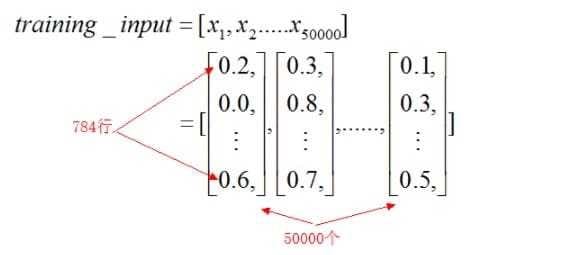

同样可以知道training_labels的样子为：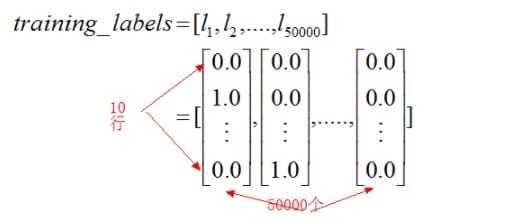

然后training_data为zip函数组合，那么training_data为一个列表，其中每个元素是一个元组，二元组又有一个training_inputs和一个training_labels的元素组合而成，如下图：

同理可以推出其他数据的形状。

三、神经网络

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
# -*- coding: utf-8 -*-
import random
import numpy as np
class Network(object):
    #初始化神经网络
    def __init__(self, sizes):
        """The list ``sizes`` contains the number of neurons in the
        respective layers of the network.  For example, if the list
        was [2, 3, 1] then it would be a three-layer network, with the
        first layer containing 2 neurons, the second layer 3 neurons,
        and the third layer 1 neuron.  The biases and weights for the
        network are initialized randomly, using a Gaussian
        distribution with mean 0, and variance 1.  Note that the first
        layer is assumed to be an input layer, and by convention we
        won't set any biases for those neurons, since biases are only
        ever used in computing the outputs from later layers."""
        self.num_layers = len(sizes)#神经网络层数
        self.sizes = sizes#储存各层神经元个数的列表
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]#随机初始化偏置
        self.weights = [np.random.randn(y, x) for x, y in zip(sizes[:-1], sizes[1:])]#随机初始化权重
    #前向传播算法
    def feedforward(self, a):
        """Return the output of the network if ``a`` is input."""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a
    #随机梯度下降（训练数据，迭代次数，小样本数量，学习率，是否有测试集（默认为无））
    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """Train the neural network using mini-batch stochastic
        gradient descent.  The ``training_data`` is a list of tuples
        ``(x, y)`` representing the training inputs and the desired
        outputs.  The other non-optional parameters are
        self-explanatory.  If ``test_data`` is provided then the
        network will be evaluated against the test data after each
        epoch, and partial progress printed out.  This is useful for
        tracking progress, but slows things down substantially."""
        if test_data:
            n_test = len(test_data)#若有测试集，则计算其大小
        n = len(training_data)#训练集大小
        #迭代过程
        for j in xrange(epochs):
            # shuffle() 方法对训练集随机排序
            random.shuffle(training_data)
            # mini_batch是列表中切割之后的列表
            mini_batches = [training_data[k:k+mini_batch_size] for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print "Epoch {0}: {1} / {2}".format(j, self.evaluate(test_data), n_test)
            else:
                print "Epoch {0} complete".format(j)
    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
        is the learning rate."""
        #存储C对于各个参数的偏导，格式和self.biases和self.weights是一模一样的
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        #mini_batch中的一个实例调用梯度下降得到各个参数的偏导
        for x, y in mini_batch:
            从一个实例得到的梯度
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        #每一个mini_batch更新一下参数
        self.weights = [w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]
    #反向传播（对于每一个实例）
    def backprop(self, x, y):
        """Return a tuple ``(nabla_b, nabla_w)`` representing the
        gradient for the cost function C_x.  ``nabla_b`` and
        ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
        to ``self.biases`` and ``self.weights``."""
        # 存储C对于各个参数的偏导，格式和self.biases和self.weights是一模一样的
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # 前向过程
        activation = x
        #存储所有的激活值，一层一层的形式
        activations = [x] # list to store all the activations, layer by layer
        #存储所有的中间值（weighted sum）
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # 反向过程
        # 输出层error
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        # 非输出层
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)
    def evaluate(self, test_data):
        """Return the number of test inputs for which the neural
        network outputs the correct result. Note that the neural
        network's output is assumed to be the index of whichever
        neuron in the final layer has the highest activation."""
        test_results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in test_data]
        return sum(int(x == y) for (x, y) in test_results)
    # 输出层cost函数对于a的导数
    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y)
#### Miscellaneous functions
#sigmoid函数
def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))
#sigmoid函数的导数
def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

四、结果比较

将隐藏层设为30层，随机梯度下降的迭代次数为30次，小批量数量大小为10，学习速率为3.0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
In [77]: import mnist_loader
In [78]: import network
In [80]: training_data,validation_data,test_data = mnist_loader.load_data_wrapper()
In [81]: net = network.Network([784,30,10])
In [82]: net.SGD(training_data,30,10,3.0,test_data = test_data)
Epoch 0: 8185 / 10000
Epoch 1: 8363 / 10000
Epoch 2: 8404 / 10000
Epoch 3: 8447 / 10000
······
Epoch 25: 9492 / 10000
Epoch 26: 9494 / 10000
Epoch 27: 9468 / 10000
Epoch 28: 9504 / 10000
Epoch 29: 9507 / 10000

经过30次迭代之后，神经网络的识别率为95%左右。



应统联盟


连接十万名应统专业同学


阿药算法


打通算法面试任督二脉