之前学习了全连接神经网络和卷积神经网络,以及它们的训练与应用。它们都只能单独的去处理单个的输入,且前后的输入之间毫无关系。但是,在一些任务中,我们需要更好的去处理序列的信息,即前后的输入之间存在关系。比如,在理解一整句话的过程中,孤立理解组成这句话的词是不够的,我们需要整体的处理由这些词连接起来的整个序列;当我们处理视频时,我们也不能单独地仅仅分析每一帧,而要分析这些帧连接起来的整个序列。这就引出了深度学习领域中另一类非常重要的神经网络:循环神经网络(Recurrent Neural Network)。
一、语言模型
RNN是在自然语言处理领域中最先使用的,如RNN可以为语言模型来建模。那么,何为语言模型?
自然语言从它产生开始,逐渐演变成一种上下文相关的信息表达和传递的方式,因此让计算机处理自然语言,一个基本的问题就是为自然语言这种上下文相关的特性建立数学模型。这个数学模型就是在自然语言处理中常说的统计语言模型(Statistical Language Model)。它最先由贾里尼克提出。
我们可以和电脑玩一个游戏,我们写出一个句子前面的一些词,然后,让电脑帮我们写下接下来的一个词,比如下面这句:
我昨天上学迟到了,老师批评了____。
我们给电脑展示了这句话前面这些词,然后让电脑写下接下来的一个词。在这个例子中,接下来的这个词最有可能是“我”,而不可能是“小明”,甚至是“吃饭”。
语言模型的出发点很简单:一个句子是否合理,就看看它的可能性大小如何。
语言模型有很多用处,比如在语音转文本(STT)的应用中,声学模型输出的结果,往往是若干个可能的候选词,这时候就需要语言模型来从这些候选词中选择一个最有可能的。当然,它同样也可以用在图像到文本的识别中(OCR技术)。
在使用RNN之前,语言模型主要是采用N-Gram。N可以是一个自然数,比如2或者3.它的含义是,假设一个词出现的概率只和前面N个词相关。我们以2-Gram为例。首先,对前面的一句话进行切词:
我 昨天 上学 迟到 了 , 老师 批评 了 ____。
如果用2-Gram进行建模,那么电脑在预测时,只会看到前面的“了”,然后,电脑会在语料库中,搜索“了”后面最有可能的一个词。不管最后电脑选的是不是“我”,这个模型看起来并不是那么靠谱,因为“了”前面的一大堆实际上丝毫没起作用。如果是3-Gram模型呢,会搜索“批评了”后面最有可能的词,看齐俩感觉比2-Gram靠谱了不少,但还是远远不够的。因为这句话最关键的信息“我”,远在9个词之前!
似乎我们可以不断提升N的值,比如4-Gram、9-Gram·······。实际上,这个想法是没有实用性的。在实际应用中最多的是N=3的三元模型,更高阶的模型就很少使用了。主要有两个原因。首先,N元模型的大小(或者说空间复杂度)几乎是N的指数函数,即$O(|V|^N)$,这里$|V|$是一种语言词典的词汇量,一般在几万到几十万个。然后,使用N元模型的速度(或者说时间复杂度)也几乎是一个指数函数,即$O(|V|^{N-1})$。因此N不能太大。当N从1到2,再从2到3时,模型的效果上升显著。而当模型从3到4时,效果的提升就不是很显著了,而资源的耗费增加却非常快,所以,除非是不惜资源为了做到极致,很少有人使用四元以上的模型。Google的罗塞塔翻译系统和语言搜索系统,使用的是四元模型,该模型存储于500台以上的Google服务器中。
RNN就解决了N-Gram的缺陷,它在理论上可以往前看(往后看)任意多个词。
二、基本循环神经网络
开始前,我们先回顾一下,简单的MLP三层神经网络模型: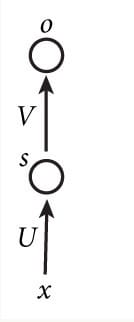
其中x是一个向量,它表示输入层的值(这里面没有画出来表示神经元节点的圆圈);s是一个向量,它表示隐藏层的值(这里隐藏层面画了一个节点,你也可以想象这一层其实是多个节点,节点数与向量s的维度相同);U是输入层到隐藏层的权重矩阵;o也是一个向量,它表示输出层的值;V是隐藏层到输出层的权重矩阵。
再看下图中一个简单的循环神经网络图,它由输入层、一个隐藏层和一个输出层组成。我们可以看到,循环神经网络的隐藏层的值s不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重矩阵W就是隐藏层上一次的值作为这一次的输入的权重。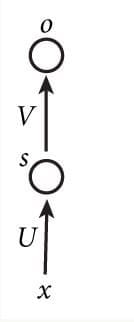
如果我们把上面的图展开,循环神经网络也可以画成下面这个样子:
现在看起来就清楚不少了,这个网络在t时刻接收到输入$X_t$之后,隐藏层的值是$S_t$,输出值是$o_t$。关键一点是,$s_t$的值不仅仅取决于$X_t$,还取决于$S_{t-1}$。我们可以使用下面的公式来表示循环神经网络的计算方法:
式1是输出层的计算公式,输出层是一个全连接层,也就是它的每个节点都和隐藏层的每个节点相连。V是输出层的权重矩阵,g是激活函数。式2是隐藏层的计算公式,它是循环层。U是输入x的权重矩阵,W是上一次的值$s_{t-1}$作为这一次的输入的权重矩阵,f是激活函数。
从上面的公式可以看出,循环层和全连接层的区别就是多了一个权重矩阵W。
若反复把式2代入带式1,我们将得到:
从上面可以看出,循环神经网络的输出值$o_t$,是受前面历次输入值$x_{t}$、$x_{t-1}$、$x_{t-2} …$的影响的,这就是为什么循环神经网络可以往前看任意多个输入值的原因。
三、双向循环神经网络
对于语言模型来说,很多时候光看前面的词是不够的,比如下面这句话:
我的手机坏了,我打算____一部新手机。
可以想象,如果我们只看横线前面的词,手机坏了,那么我是打算修一修?换一部新的?还是大哭一场?这些都是无法确定的,但是如果我们也看到了后面的词是“一部新手机”,那么横线上的词填“买”的概率就大很多了。
而这个在单向循环神经网络是无法建模的,因此我们需要双向循环神经网络,如下图所示: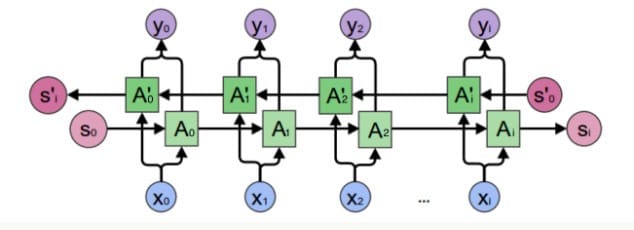
我们先考虑$y_2$的计算,从上图可以看出,双向卷积神经网络的隐藏层要保存两个值,一个A参与正向计算,另一个$A’$参与反向计算。最终的输出值$y_2$取决于$A_2$和$A_2’$,其计算方法为:
$A_2$和$A_2’$则分别计算:
现在,我们已经可以看出一般的规律:正向计算时,隐藏层的值$s_t$与$s_{t-1}$有关;反向计算时,隐藏层的值$s_t’$与$s_{t+1}’$有关;最终的输出取决于正向和反向计算的加和。现在,我们仿照式1和式2,写出双向循环神经网络的计算方法:
从上面三个公式我们可以看到,正向计算和反向计算不共享权重,也就是说$U$和$U’$、$W$和$W’$、$V$和$V’$都是不同的权重矩阵。
四、深度循环神经网络
前面我们介绍的循环神经网络只有一个隐藏层,我们当然也可以堆叠两个以上的隐藏层,这样就得到了深度循环神经网络。如下图所示:
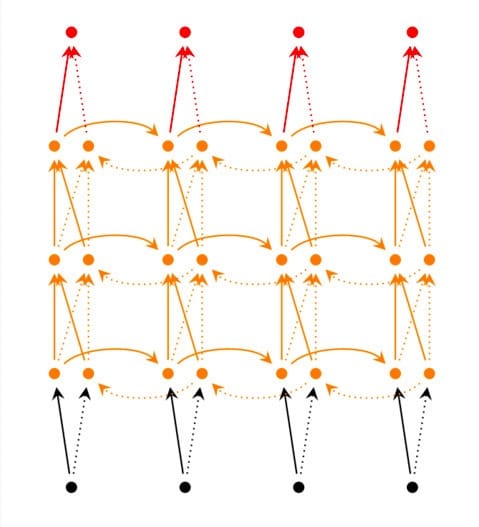
我们把第$i$个隐藏层的值表示为$s_t^{(i)}、s_t^{‘(i)}$,则深度循环神经网络的计算方式可以表示为:
五、循环神经网络的训练算法:BPTT
BPTT算法是针对循环层的训练算法,它的基本原理和BP算法是一样的,也包含同样的三个步骤:
- 1)前向计算每个神经元的输出值;
- 2)反向计算每个神经元的误差项$\delta_j$,它是误差函数E对神经元$j$的加权输入$net_j$的偏导数;
- 3)计算每个权重的梯度。
- 4)最后再用随机梯度下降算法更新权重。
循环层如下图所示: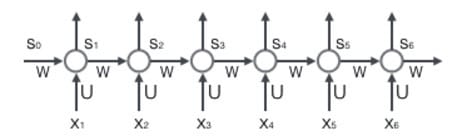
5.1 前向计算
使用前面的式2对循环层进行前向计算:
注意,上面的$s_t、x_t、s_{t-1}$都是向量,用黑体字表示;而$U、V$是矩阵,用大写字母表示。向量的下标表示时刻,例如,$s_t$表示在$t$时刻向量$s$的值。
我们假设输入向量x的维度是$m$,输出向量的维度是$n$,则矩阵$U$的维度是$n×m$,矩阵$W$的维度是$n×n$。下面是上式展开成矩阵的样子,看起来更直观一点:
在这里我们用手写体字母表示向量的一个元素,它的下标表示它是这个向量的第几个元素,它的上标表示第几个时刻。例如,$s_j^t$表示向量$s$的第$j$个元素在$t$时刻的值。$u_{ji}$表示输入层第$i$个神经元到循环层第$j$个神经元的权重。$w_{ji}$表示循环层第$t-1$时刻的第$i$个时刻的第$j$个神经元的权重。
5.2 误差项的计算
BTPP算法将第$l$层$t$时刻的误差项$\delta _t^l$值沿两个方向传播,一个方向是其传递到上一层网络,得到$\delta _t^{l-1}$,这部分只和权重矩阵$U$有关;另一个方向是将其沿着时间线传递到初始$t_1$时刻,得到$\delta_1^l$,这部分只和权重矩阵$W$有关。
我们用向量$net_j$表示神经元在$t$时刻的加权输入,因为:
因此:
我们用$a$表示列向量,用$a^T$表示行向量。上式的第一项是向量函数对向量求导,其结果为Jacobian矩阵:
上式第二项也是一个jacobian矩阵:
最后,将俩项合在一起,可得:
上式描述了将$\delta$沿时间往前传递一个时刻的规律,有了这个规律,我们就可以求得任意时刻$k$的误差项$\delta_k$:
这个就是将误差项沿着时间反向传播的算法。
循环层将误差项反向传递到上一层网络,与普通的全连接层是完全一样的,在此简要描述一下:
循环曾的加权输入$net^l$与上一层的加权输入$net^{l-1}$关系如下:
上式中$net_t^l$是第$l$层神经元的加权输入(假如第$l$是循环层);$net_t^{l-1}$是$l-1$层神经元的加权输入;$a_t^{l-1}$是第$l-1$层神经元的输出;$f^{l-1}$是第$l-1$层的激活函数。
所以
上式就是将误差项传递到上一层算法。
5.3 权重梯度的计算
接下来是BPTT算法的最后一步:计算每个权重的梯度。
首先我们计算误差函数$E$对权重矩阵$W$的梯度
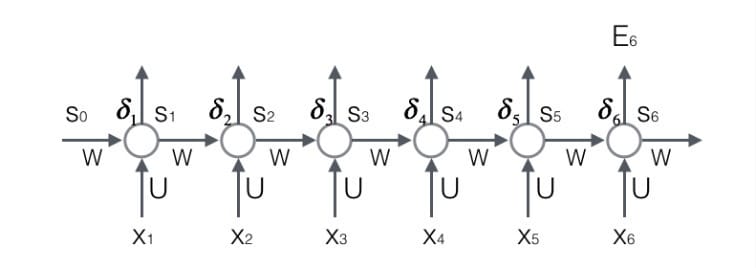
上图展示了我们到目前为止,在前两步中已经计算得到的量,包括每个时刻$t$循环层的输出值$s_t$,以及误差项$\delta_t$。
我们只要知道了任意一个时刻的误差项$\delta_t$,以及上一个时刻循环层的输出值$s_{t-1}$,就可以按照下面的公式求出权重矩阵在$t$时刻的梯度:
上式中,$\delta_i^t$表示$t$时刻误差项向量的第$i$个分量;$s_i^{t-1}$表示$t-1$时刻循环层第$i$个神经元的输出值。
下面我们简单推导一下上式。
我们知道
因为对$W$求导与$Ux_t$无关,我们不加考虑。现在,我们考虑对权重项$w_{ji}$求导。通过观察上式我们可以看到$w_{ji}$只与$net^t_j$有关,所以:
按照这个规律就可以生成梯度矩阵$\nabla_{w_t}E$了。
我们已经求得权重矩阵$W$在$t$时刻的梯度$\nabla_{w_t}E$,最终的梯度$\nabla_{w_t}E$是各个时刻的梯度之和:
这就是计算循环曾权重矩阵$W$的梯度的公式。
前面介绍了权重梯度的计算方法,看上去比较直观。但为什么最终的梯度的是各个时刻的梯度之和呢?我们前面只是直接用了这个结论,实际上这里面是有道理的。
我们从这个式子开始:因为$Ux_t$与$W$完全无关,我们把它看做常量。现在,考虑第一个式子加号右边的部分,因为$W$和$f(net_{t-1})$都是$W$的函数,所以,对其求偏导得到:
我们最终需要计算的是
我们先计算加号左边的部分。$\frac{\partial W}{\partial W}$是矩阵对矩阵求导,其结果是一个四维张量(tensor),如下所示:
接下来,我们知道$s_{t-1=f(net_{t-1})}$,它是一个列向量。我们让上面的四维张量与这个向量相乘,得到了一个三维张量,再左乘行向量$\delta_t^T$,最终得到一个矩阵:
接下来,我们计算加号右边的部分:
我们得到了如下递推公式:
与权重矩阵$W$类似,我们可以得到权重矩阵$U$的计算方法。
它是误差函数在$t$时刻对权重矩阵$U$的梯度。和权重矩阵$W$一样,最终的梯度也是各个时刻的梯度之和:
具体地证明与上述类似。
六、梯度爆炸与梯度消失
不幸的是,实践中前面介绍的集中RNNs并不能很好地处理较长的序列。一个主要的原因是,RNN在训练中很容易发生梯度爆炸和梯度消失,这导致训练时梯度不能再较长序列中一直传递下去,从而使RNN无法捕捉到长距离的影响。
为什么RNN会产生梯度爆炸和梯度消失问题呢?我们根据下式来分析。之前推导过程中得到:
上式的$\beta$定义为矩阵的模的上界。因为上式是一个指数函数,如果$t_k$很大的话(也就是向前看得很远的时候),会导致对应的误差项的值增长或缩小的非常快,这样就会导致相应的梯度爆炸和梯度消失问题(取决于$\beta$大于1还是小于1)。
通常来说,梯度爆炸更容易处理一些。因为梯度爆炸时,我们的程序会收到NaN的错误。我们也可以设置一个梯度阈值,当梯度超过这个阈值的时候可以直接截取。
梯度消失更难检测,而且也更难处理一些。总的来说,我们有三种方法应对梯度消失问题:
- 1)合理的初始化权重值。初始化权重,使每个神经元尽可能不要取极大或极小值,以躲开梯度消失的区域。
- 2)使用ReLu代替sigmoid和tanh作为激活函数。
- 3)使用其他结构的RNNs,比如长短时记忆网络(LSTM)和Gated Recurrenr Unit(GRU),这是最流行的做法。
纠错词:

