深度学习系列（6）：递归神经网络

上一篇我们学习了循环神经网络，它可以用来处理包含序列的信息。然而，除此之外，信息往往还存在着诸如树结构、图结构等更复杂的结构。对于这种复杂的结构。循环神经网络就无能为力了。本文学习一种更为强大、复杂的神经网络：递归神经网络（Recursive Neural NetWork，RNN），以及它的训练算法BPTS（Back Propagation Through Structure）。顾名思义，递归神经网络可以处理诸如树、图这样的递归网络。

一、递归神经网络的定义

因为神经网络的输入层单元个数是固定的，因此必须用循环或者递归的方式来处理长度可变的输入。循环神经网络实现了前者，通过将长度不定的输入分割为等长度的小块，然后再依次的输入到网络中，从而实现了神经网络对变长输入的处理。一个典型的例子是，当我们处理一句话的时候，我们可以把一句话看作是词组成的序列，然后，每次向循环神经网络输入一个词，如此循环直至整句话输入完毕，循环神经网络将产生对应的输出。如此，我们就能处理任意长度的句子了。
如下图所示：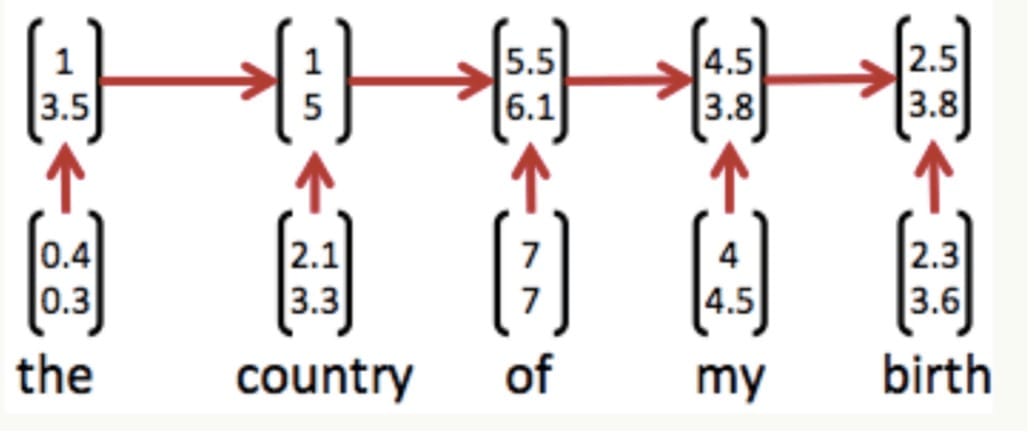

然而，有时候把句子看作是词的序列是不够的，比如下面这句话“两个外语学院的学生”：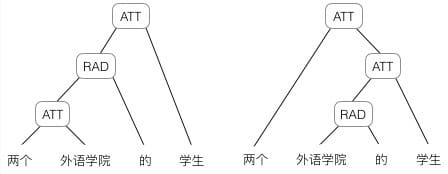

上图显示了这句话的两个不同的语法解析树。可以看出这句话有歧义，不同的语法解析树则对应了不同的意思。一个是『两个外语学院的/学生』，也就是学生可能有许多，但他们来自于两所外语学校；另一个是『两个/外语学院的学生』，也就是只有两个学生，他们是外语学院的。为了能够让模型区分出两个不同的意思，我们的模型必须能够按照树结构去处理信息，而不是序列，这就是递归神经网络的作用。当面对按照树/图结构处理信息更有效的任务时，递归神经网络通常都会获得不错的结果。

递归神经网络可以把一个树、图结构信息编码为一个向量，也就是把信息映射到一个语义向量空间中。这个语义向量空间满足某类性质，比如语义相似的向量距离更近。也就是说，如果两句话（尽管内容不容）它的意思是相似的，那么把它们分别编码后的两个向量的距离也更近；反之，如果两句话的意思截然不同，那么编码后的距离则更远。如下图所示：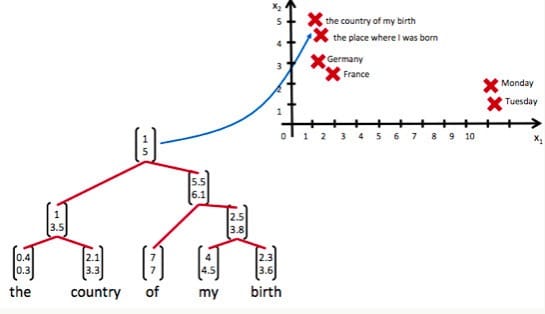

从上图我们可以看到，递归神经网络将所有的词、句都映射到一个2维向量空间中。句子“the country of my birth”和句子“the place where I was born”的意思是非常接近的，所以表示它们的两个向量在向量空间中的距离很近。另外两个词“Germany”和“France”因为表示的都是地点，它们的向量与上面两句话的向量的距离，就比另外两个表示时间的词“Monday”和“Tuesday”的向量的距离近得多。这样，通过向量的距离，就得到了一种语义的表示。

上图还显示了自然语言可组合的性质：词可以组成句、句可以组成段落、段落可以组成篇章，而更高层的语义取决于底层的语义以及它们的组合方式。递归神经网络是一种表示学习，它可以将词、句、段、篇按照他们的语义映射到同一个向量空间中，也就是把可组合（树/图结构）的信息表示为一个个有意义的向量。比如上面这个例子，递归神经网络把句子”the country of my birth”表示为二维向量[1,5]。有了这个『编码器』之后，我们就可以以这些有意义的向量为基础去完成更高级的任务（比如情感分析等）。如下图所示，递归神经网络在做情感分析时，可以比较好的处理否定句，这是胜过其他一些模型的：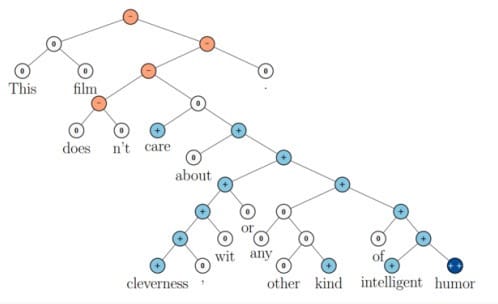

在上图中，蓝色表示正面评价，红色表示负面评价。每个节点是一个向量，这个向量表达了以它为根的子树的情感评价。比如”intelligent humor”是正面评价，而”care about cleverness wit or any other kind of intelligent humor”是中性评价。我们可以看到，模型能够正确的处理doesn’t的含义，将正面评价转变为负面评价。

尽管递归神经网络具有更为强大的表示能力，但是在实际应用中并不太流行。其中一个主要原因是，递归神经网络的输入是树/图结构，而这种结构需要花费很多人工去标注。想象一下，如果我们用循环神经网络处理句子，那么我们可以直接把句子作为输入。然而，如果我们用递归神经网络处理句子，我们就必须把每个句子标注为语法解析树的形式，这无疑要花费非常大的精力。很多时候，相对于递归神经网络能够带来的性能提升，这个投入是不太划算的。

二、递归神经网络的前向计算

接下来，我们详细介绍一下递归神经网络是如何处理树/图结构的信息的。在这里，我们以处理树型信息为例进行介绍。

递归神经网络的输入是两个子节点（也可以是多个），输出就是将这两个子节点编码后产生的父节点，父节点的维度和每个子节点是相同的。如下图所示：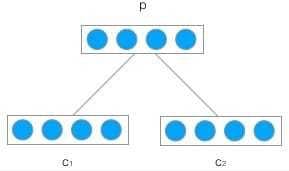

$c_1$和$c_2$分别是表示两个子节点的向量，$p$是表示父节点的向量。子节点和父节点组成一个全连接神经网络，也就是子节点的每个神经元都和父节点的每个神经元两两相连。我们用矩阵$W$表示这些连接上的权重，它的维度将是$d×2d$，其中，$d$表示每个节点的维度。父节点的计算公式可以写成：

$$p=\tan\textrm{h}\left(W\left[\begin{array}{c} c_1\\ c_2\\ \end{array}\right]+b\right)$$

在上式中，tanh是激活函数（当然也可以用其它的激活函数），是偏置项，它也是一个维度为的向量。

然后，我们把产生的父节点的向量和其他子节点的向量再次作为网络的输入，再次产生它们的父节点。如此递归下去，直至整棵树处理完毕。最终，我们将得到根节点的向量，我们可以认为它是对整棵树的表示，这样我们就实现了把树映射为一个向量。在下图中，我们使用递归神经网络处理一棵树，最终得到的向量$p_3$，就是对整棵树的表示：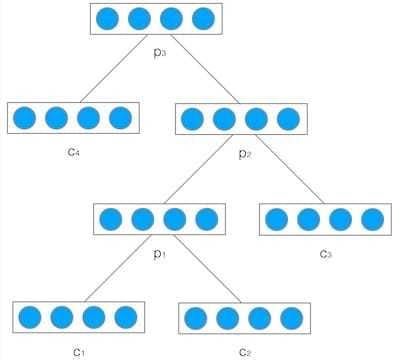

举个例子，我们使用递归神将网络将”两个外语学校的学生”映射为一个向量，如下图所示：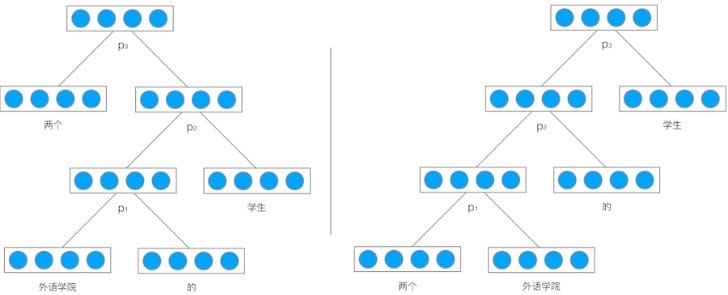

最后得到的向量$p_3$就是对整个句子”两个外语学校的学生”的表示。由于整个结构是递归的，不仅仅是根节点，事实上每个节点都是以其为根的子树的表示。比如，在左边的这棵树中，向量$p_2$是短语”外语学院的学生”的表示，而向量$p_1$是短语”外语学院的”的表示。

$$p=\tan\textrm{h}\left(W\left[\begin{array}{c} c_1\\ c_2\\ \end{array}\right]+b\right)$$

该式就是递归神经网络的前向计算算法，它和全连接神经网络没有什么区别，只是在输入的过程中需要根据输入的树结构依次输入每个子节点。

需要特别注意的是，递归神经网络的权重$W$和偏置项$b$在所有节点都是共享的。

三、递归神经网络的训练

递归神经网络的训练算法和循环神经网络类似，两者不同之处在于，前者需要将残差$\delta$从根节点反向传播到各个子节点，而后者是将残差$\delta$从当前时刻$t_k$反向传播到初始时刻$t_1$。

下面，我们介绍适用于递归神经网络的训练算法，也就是BPTS算法。

3.1 误差项的传递

首先，我们先推导将误差从父节点传递到子节点的公式，如下图：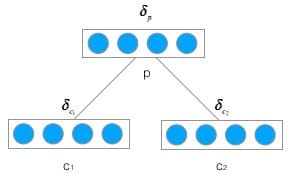

定义$\delta_p$为误差函数E相对于父节点$p$的加权输入$net_p$的导数，即：

$$\delta_p=\frac{\partial E}{\partial net_p}$$

设$net_p$是父节点的加权输入，则

$$net_p=W\left[\begin{array}{c} c_1\\ c_2\\ \end{array}\right]+b$$

在上述式子里，$net_p、c_1、c_2$都是向量，而$W$是矩阵。为了看清楚它们的关系，我们将其展开：

$$\left[\begin{array}{c} net_{p1}\\ net_{p2}\\ ···\\ net_{pn}\\ \end{array}\right]=\left[\begin{matrix} w_{p1c11}& w_{p1c12}& ···& w_{p1c21}···\\ w_{p2c11}& w_{p2c12}& ···& w_{p2c21}···\\ ···& ···& ···& ···\\ w_{pnc11}& w_{pnc12}& ···& w_{pnc21}···\\ \end{matrix}\right]\left[\begin{array}{c} net_{c11}\\ net_{c12}\\ ···\\ net_{c21}\\ net_{c22}\\ ···\\ \end{array}\right]$$

在上面的公式中，$p_i$表示父节点$p$的第i个分量；$c_{1i}$表示子节点的第i个分量；$c_{2i}$表示$c_2$子节点的第$i$个分量；$w_{p_ic_{jk} }$表子节点$c_j$的第k个分量到父节点p的第i个分量的权重。根据上面展开后的矩阵乘法形式，我们不难看出，对于子节点$c_{jk}$来说，它会影响父节点所有的分量。因此，我们求误差函数E对$c_{jk}$的导数时，必须用到全导数公式，也就是：

$$\frac{\partial E}{\partial c_{jk}}=\sum_i{\frac{\partial E}{\partial net_{p_i}}\frac{\partial net_{p_i}}{\partial c_{jk}}}=\sum_i{\delta_{p_i}w_{p_ic_{jk}}}$$

有了上式，我们就可以把它表示为矩阵形式，从而得到一个向量化表达：

$$\frac{\partial E}{\partial c_j}=U_j\delta_p$$

其中，矩阵$U_j$是从矩阵$W$中提取部分元素组成的矩阵。其单元为$u_{j_{ik}}=w_{p_k}c_{ji}$上式看上出可能有点抽象，从下图，我们可以直观的看到$U_j$到底是啥。首先我们把$W$矩阵拆分为两个矩阵$W_1$和$W_2$，如下图所示：

显然，子矩阵$W_1$和$W_2$分别对应子节点$c_1$和$c_2$的到父节点$p$权重。则矩阵$U_j$为：

$$U_j=W_j^T$$

也就是说，将误差项反向传递到相应子节点$c_j$的矩阵$U_j$就是其对应权重矩阵$W_j$的转置。

现在，我们设$net_{c_j}$是子节点$c_j$的加权输入，$f$是子节点$c$的激活函数，则：

$$c_j=f(net_{c_j})$$

这样，我们得到：

$$\delta_{c_j}=\frac{\partial E}{\partial net_{c_j}}=\frac{\partial E}{\partial c_j}\frac{\partial c_j}{\partial net_{c_j}}=W_{j}^{T}\delta_p°f'\left(net_{c_j}\right)$$

如果我们将不同子节点$c_j$对应的误差项$\delta_{c_j}$连接成一个向量

$$\delta_c=\left[\begin{array}{c} \delta_{c_1}\\ \delta_{c_2}\\ \end{array}\right]$$

那么，上式可以写成

$$\delta_c=W^T\delta_p°f'\left(net_c\right)$$

它就是将误差项从父节点传递到其子节点的公式。注意上式中的$net_c$也是将两个子结点的加权输入$net_{c_1}$和$net_{c_2}$连在一起的向量。
有了传递一层的公式，我们就不难写出逐层传递的公式。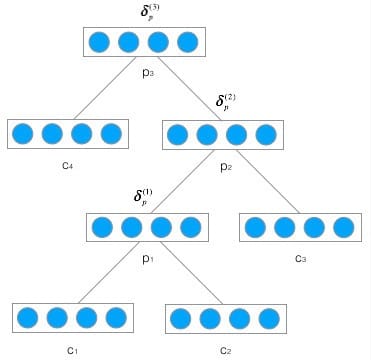

上图是在树型结构中反向传递项的全景图，反复应用上式，在已知$\delta_p^{(3)}$的情况下，我们不难算出$\delta_p^{(1)}$为：

$$\delta^{\left(2\right)}=W^T\delta_{p}^{\left(3\right)}°f'\left(net^{\left(2\right)}\right)$$ $$\delta_{p}^{\left(2\right)}=\left[\delta^{\left(2\right)}\right]_p$$ $$\delta^{\left(1\right)}=W^T\delta_{p}^{\left(2\right)}°f'\left(net^{\left(1\right)}\right)$$ $$\delta_{p}^{\left(1\right)}=\left[\delta^{\left(1\right)}\right]_p$$

在上面的公式中

$$\delta^{\left(2\right)}=\left[\begin{array}{c} \delta_{c}^{\left(2\right)}\\ \delta_{p}^{\left(2\right)}\\ \end{array}\right]$$

$\left[\delta^{\left(2\right)}\right]_p$表示取向量$\delta^{(2)}$属于节点p的部分。

3.2 权重梯度的计算

根据加权输入的计算公式：

$$net_p^{(l)}=Wc^{(l)}+b$$

其中，$net_p^{(l)}$表示第$l$层的父节点的加权输入，$c^{(l)}$表示第$l$层的子节点。W是权重矩阵，$b$是偏置项，将其展开可得：

$$net_{p_j}^{l}=\sum_i{w_{ji}c_{i}^{l}}+b_j$$

那么，我们可以求得误差函数在第$l$层对权重的梯度为：

$$\frac{\partial E}{\partial w_{ji}^{\left(l\right)}}=\frac{\partial E}{\partial net_{p_j}^{\left(l\right)}}\frac{\partial net_{p_j}^{\left(l\right)}}{\partial w_{ji}^{\left(l\right)}}=\delta_{p_j}^{\left(l\right)}·c_{i}^{\left(l\right)}$$

上式是针对一个权重项$w_{ji}$的公式，现在需要把它扩展为对所有的权重项的公式。我们可以把上式写成写成矩阵的形式（在下面的公式中，m=2n）:

$$\frac{\partial E}{\partial W^{\left(l\right)}}=\delta^{\left(l\right)}·\left(c^{\left(l\right)}\right)^T$$

这就是第$l$层权重项的梯度计算公式。我们知道，由于权重$W$是在所有层共享的，所以和循环神经网络一样，递归神经网络的最终权重梯度是各个层权重梯度之和。即：

$$\frac{\partial E}{\partial W}=\sum_l{\frac{\partial E}{\partial W^{\left(l\right)}}}$$

和循环神经网络一样，递归神经网络最终梯度之和是各层梯度之和。

接下来，我们求偏置项$b$的梯度计算公式。先计算误差函数对第$l$层偏置项$b^{(l)}$的梯度：

$$\frac{\partial E}{\partial b_{j}^{\left(l\right)}}=\frac{\partial E}{\partial net_{p_j}^{\left(l\right)}}\frac{\partial net_{p_j}^{\left(l\right)}}{\partial b_{j}^{\left(l\right)}}=\delta_{p_j}^{\left(l\right)}$$

把上式扩展为矩阵的形式：

$$\frac{\partial E}{\partial b^{\left(l\right)}}=\delta_{p}^{\left(l\right)}$$

最终的偏置项梯度是各个层偏置项梯度之和，即：

$$\frac{\partial E}{\partial b}=\sum_l{\frac{\partial E}{\partial b^{\left(l\right)}}}$$

3.3 权重更新

如果使用梯度下降优化算法，那么权重更新公式为：

$$W\gets W+\eta\frac{\partial E}{\partial W}$$

其中，$\eta$是学习速率常数。把之前的式子代入上式，即可完成权重的更新。同理，偏置项的更新公式为：

$$b\gets b+\eta\frac{\partial E}{\partial b}$$

同样把之前求得式子代入上式，即可完成偏置项的更新。

这就是递归神经网络的训练算法BPTS。