深度学习系列（8）：激活函数

深度学习的基本原理是基于人工神经网络，信号从一个神经元进入，经过非线性的activation function，传入到下一层神经元；再经过该层神经元的activate function，继续往下传递，如此循环往复，直到输出层。其中的激活函数的主要作用是提供网络的非线性建模能力，使得神经网络有足够的capacity来抓取复杂的pattern，在各个领域取得state-of-the-art的结果。

现在假设一个神经网络中仅包含线性激励和全连接运算，那么该网络仅仅能够表达线性映射，即使增加网络的深度也依旧还是线性映射，即输出都是输入的线性组合，失去了隐藏层存在的意义，难以有效建模实际环境中非线性分布的数据。加入非线性激活函数之后，深度学习网络可以逼近任意函数，具备了分层的非线性映射学习能力。加拿大蒙特利尔大学的Bengio教授在 ICML 2016 的文章中给出了激活函数的定义：激活函数是映射 h:R→R，且几乎处处可导。从定义来看，几乎所有连续可导函数都可以用作激活函数。但目前常见的多是分段线性和具有指数形状的非线性函数。

显而易见，activation function在深度学习中举足轻重，也是很活跃的研究领域之一。目前来讲，选择怎样的activation function不在于它能否模拟真正的神经元，而在于能否便于优化整个深度神经网络。

一、软饱和与硬饱和激活函数

Bengio 教授等将具有

• 1）在定义域内处处可导
• 2）两侧导数逐渐趋近于0，即$\lim_{x\rightarrow\infty}f’\left(x\right)=0$。
  的激活函数定义为软饱和激活函数。

与极限的定义类似，饱和也分为左饱和与右饱和，左侧软饱和为：

$$\lim_{x\rightarrow -\infty}f'\left(x\right)=0$$

右侧软饱和为：

$$\lim_{x\rightarrow +\infty}f'\left(x\right)=0$$

与软饱和激活函数相对的是硬饱和激活函数，即：

$$f'(x)=0, 当|x|>c,c为常数$$

同理，应饱和也分为左饱和与右饱和，左侧硬饱和为：

$$f'(x)=0, 当-x>c, c为正数$$

右侧硬饱和为：

$$f'(x)=0, 当x>c, c为正数$$

二、sigmoid

sigmoid非线性函数的数学公式为：

$$\sigma\left(x\right)=\frac{1}{1+e^{-x}}$$

函数图像及梯度函数图像如下所示：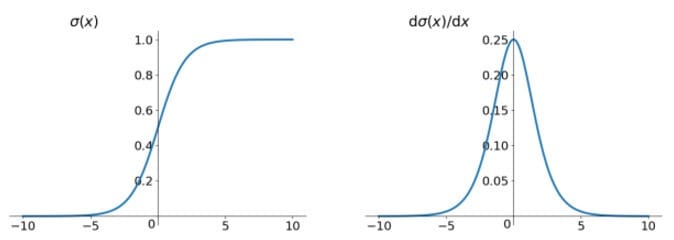

它将输入实数值“挤压”到0-1范围内。更具体地说，很大的负数变成0，很大的正数变成1。它是便于求导的平滑函数，其导数为$\sigma(x)(1-\sigma(x))$，这是它的优点。sigmoid 在定义域内处处可导，且两侧导数逐渐趋近于0，即：$\lim_{x\rightarrow\infty}f’\left(x\right)=0$

然而现在sigmoid函数已经不太受欢迎，实际很少使用了，这是因为它有三个主要缺点：

• 1）梯度消失。Sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。具体地，我们知道优化神经网络的方法是Back Propagation，即导数的反向传递：先计算输出层对应的loss，然后将loss以导数的形式不断向上一层网络传递，修正相应的参数，达到降低loss的目的。sigmoid反向传导的梯度包含了一个f’(x) 因子（sigmoid关于输入的导数），因此一旦输入落入饱和区，f’(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说， sigmoid 网络在 5 层之内就会产生梯度消失现象。我们也可以在图中看出原因，主要在于两点：(1) 在上图中容易看出，当$\sigma(x)$中x较大或较小时，导数接近0，而后向传递的数学依据是微积分求导的链式法则，当前层的导数需要之前各层导数的乘积，几个小数的相乘，结果会很接近0 (2) Sigmoid导数的最大值是0.25，这意味着导数在每一层至少会被压缩为原来的1/4，通过两层后被变为1/16，…，通过10层后为1/1048576。请注意这里是“至少”，导数达到最大值这种情况还是很少见的。梯度消失问题至今仍然存在，但被新的优化方法有效缓解了，例如DBN中的分层预训练，Batch Normalization的逐层归一化，Xavier和MSRA权重初始化等代表性技术。

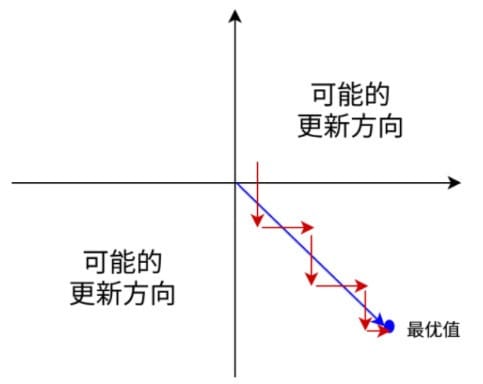
• 2）Sigmoid函数的输出不是Zero-centered的。这个性质并不是我们想要的，因为在神经网络后面层中的神经元得到的数据将不是零中心的。这一情况将影响梯度下降的运作，因为如果输入神经元的数据总是正数(比如在$f=w^Tx+b$中每个元素都x>0),那么关于w的梯度在反向传播的过程中，将会要么全部是正数，要么全部是负数（具体依整个表达式f而定）。这将会导致梯度下降权重更新时出现z字型的下降（如下图所示）。然而，可以看到整个批量的数据的梯度被加起来后，对于权重的最终更新将会有不同的正负，这样就从一定程度上减轻了这个问题。因此，该问题相对于上面的神经元饱和问题来说只是个小麻烦，没有那么严重。

• 3）幂运算相对耗时：相对于前两项，这其实并不是一个大问题，我们目前是具备相应计算能力的，但面对深度学习中庞大的计算量，最好是能省则省。之后我们会看到，在ReLU函数中，需要做的仅仅是一个thresholding，相对于幂运算来讲会快很多。

三、tanh

tanh非线性函数的数学公式为：

$$tanh x = \frac{e^x-e^{-x}}{e^x+e^{-x}}$$

函数图像及梯度函数图像如下所示：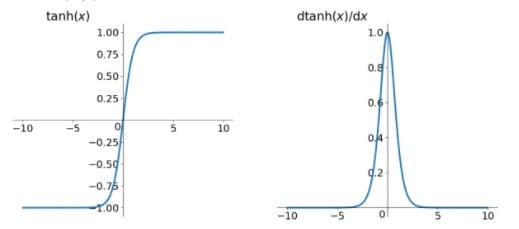
如上图所示，计算可以知道：$tanh(x)=2sigmoid(2x)-1$，它其实是一个简单放大的sigmoid神经元，和sigmoid神经元一样，也具有软饱和性。但是和sigmoid神经元不同的是，它解决了zero-centered的输出问题，因此，在实际操作中，tanh非线性函数比sigmoid非线性函数更受欢迎。然而，gradient vanishing的问题和幂运算的问题仍然存在。Xavier在文献[]中分析了sigmoid与tanh的饱和现象及特点，具体见原论文。此外，文献[]中提到了tanh网络的收敛速度要比sigmoid块。因为tanh的输出均值比sigmoid更接近0，SGD会更接近natural gradient（一种二次优化技术），从而降低所需的迭代次数。

四、ReLU

ReLU非线性函数的数学公式为：

$$ReLU(x)=max(0,x)$$

函数图像及梯度函数图像如下所示：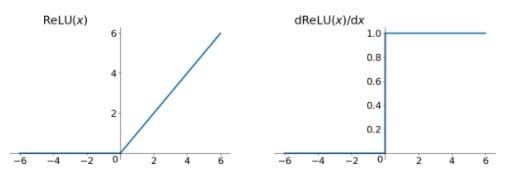
虽然2006年Hinton教授提出通过分层无监督预训练解决深层网络训练困难的问题，但是深度网络的直接监督式训练的最终突破，最主要的原因是新型激活函数ReLU。它有以下几大优点：

• 1）解决了gradient vanishing问题：ReLU在$x<0$时硬饱和。由于$x>0$时导数为1，所以，ReLU能够在$x>0$时保持梯度不衰减，从而缓解梯度消失问题。
• 2）计算速度非常快。对比sigmoid和tanh神经元含有指数运算等耗费计算资源的操作，ReLU可以简单地通过对一个矩阵进行阈值计算得到。
• 3）收敛速度非常快。相较于sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用。下图是从 Krizhevsky 等的论文中截取的图表，指明使用ReLU比使用tanh的收敛快6倍。
  
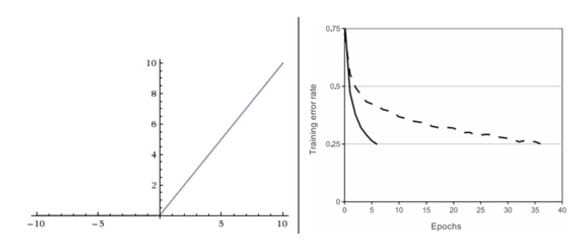
• 4）ReLU另外一个性质是提供神经网络的稀疏表达能力，在Bengio教授的Deep Sparse Rectifier Neural Network[6]一文中被认为是ReLU带来网络性能提升的原因之一。但后来的研究发现稀疏性并非性能提升的必要条件，文献 RReLU [9]也指明了这一点。
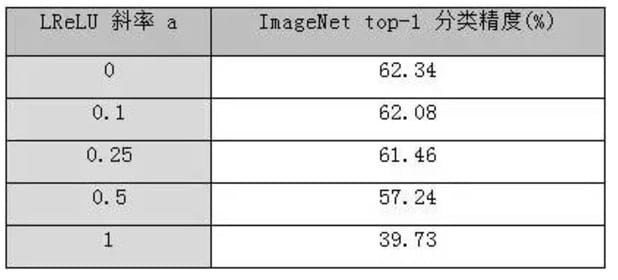
  • PReLU[10]、ELU[7]等激活函数不具备这种稀疏性，但都能够提升网络性能。本文作者在文章[8]中给出了一些实验比较结果。首先，在cifar10上采用NIN网络，实验结果为 PReLU > ELU > ReLU，稀疏性并没有带来性能提升。其次，在 ImageNet上采用类似于[11] 中model E的15 层网络，实验结果则是ReLU最好。为了验证是否是稀疏性的影响，以 LReLU [12]为例进一步做了四次实验，负半轴的斜率分别为1，0.5，0.25, 0.1，需要特别说明的是，当负半轴斜率为1时，LReLU退化为线性函数，因此性能损失最大。实验结果展现了斜率大小与网络性能的一致性。综合上述实验可知，ReLU的稀疏性与网络性能之间并不存在绝对正负比关系。

ReLU也有几个缺点：

• 1）Dead ReLU Problem。随着训练的推进，部分输入会落入硬饱和区，某些神经元可能永远不会被激活，这个ReLU单元在训练中将不可逆转的死亡，导致相应的参数永远不能被更新，使得数据多样化丢失。这种现象被称为“神经元死亡”。有两个主要原因可能导致这种情况产生: (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。例如，如果学习率设置得太高，可能会发现网络中40%的神经元都会死掉（在整个训练集中这些神经元都不会被激活）。解决方法是可以采用Xavier初始化方法，以及避免将learning rate设置太大或使用adagrad等自动调节learning rate的算法。
• 2）偏移现象。即输出均值恒大于零。偏移现象和Dead ReLU Problem会共同影响网络的收敛性。

尽管存在上述几个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

五、Leaky ReLU

Leaky ReLU非线性函数的数学公式为：

$$f(x)=max(0.01x,x)$$

函数图像及梯度函数图像如下所示：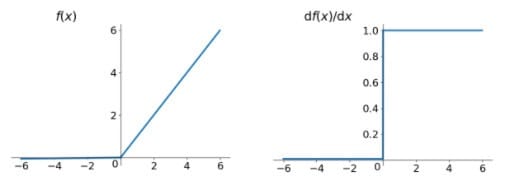
人们为了解决Dead ReLU Problem，提出了将ReLU的前半段设为0.01x而非0。
理论上来说，Leaky ReLU拥有ReLU的所有优点，外加不会有Dead ReLU problem，但是在实际操作中，并没有完全证明Leaky ReLU总是好于ReLU。有些研究者的论文指出这个激活函数表现很不错，但是其效果并不是很稳定。

六、PReLU

Parametric ReLU非线性函数的数学公式为：

$$f(x)=max(\alpha x,x)$$

PReLU是ReLU和LReLU的改进版本，具有非饱和性。与LReLU相比，PReLU中的负半轴斜率$\alpha$由back propagation学习而非固定。原文献建议初始化$\alpha$为0.25，不采用正则。

虽然PReLU 引入了额外的参数，但基本不需要担心过拟合。例如，在cifar10+NIN实验中， PReLU比ReLU和ELU多引入了参数，但也展现了更优秀的性能。所以实验中若发现网络性能不好，建议从其他角度寻找原因。

与ReLU相比，PReLU收敛速度更快。因为PReLU的输出更接近0均值，使得SGD更接近natural gradient。证明过程参见原文[10]。

七、RReLU

数学形式与PReLU类似，但RReLU[9]是一种非确定性激活函数，其参数是随机的。这种随机性类似于一种噪声，能够在一定程度上起到正则效果。作者在cifar10/100上观察到了性能提升。

综上，ReLU家族讲完了，总结如下图：

其中表格为在cifar10上采用NIN网络的实验结果。

八、Maxout

Maxout[13]是ReLU的推广，其发生饱和是一个零测集事件（measure zero event）。正式定义为：

$$max(w_1^Tx+b_1,w^T_2+b_2,···,w_n^Tx+b_n)$$

Maxout网络能够近似任意连续函数，且Maxout是对ReLU和leaky ReLU的一般化归纳，当$w_2,b_2,···,w_n,b_n$为0时，退化为ReLU。其实，Maxout的思想在视觉领域存在已久。例如，在HOG特征里有这么一个过程：计算三个通道的梯度强度，然后在每一个像素位置上，仅取三个通道中梯度强度最大的数值，最终形成一个通道。这其实就是Maxout的一种特例。

所以Maxout神经元就拥有ReLU单元的所有优点（线性操作和不饱和，能够缓解梯度消失），而没有它的缺点（死亡的ReLU单元）。然而和ReLU对比，它每个神经元的参数数量增加了一倍，这就导致整体参数的数量激增。

九、ELU

ELU（Exponential Linear Units）非线性函数的数学公式为：

$$f(x)=max(0,x)+\alpha·min(0,exp(x)-1)$$

函数图像及梯度函数图像如下所示：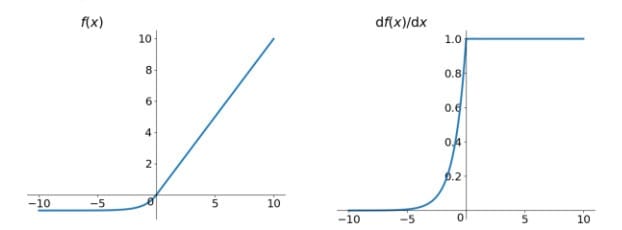
ELU也是为解决ReLU存在的问题而提出，显然，ELU有ReLU的基本所有优点，并有自身的特点，罗列如下：

• 1）右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱和能够燃ELU对输入变换或噪声更加鲁棒。
• 2）ELU的输出均值接近于零，即zero-centered，所以收敛速度更快。经ELU的作者实验，ELU的收敛性质的确优于ReLU和PReLU。在cifar10上，ELU 网络的loss 降低速度更快；在 ImageNet上，不加 Batch Normalization 30 层以上的 ReLU 网络会无法收敛，PReLU网络在MSRA的Fan-in （caffe ）初始化下会发散，而 ELU 网络在Fan-in/Fan-out下都能收敛 。

它的一个小问题在于计算量稍大，类似于Leaky ReLU，理论上虽然好于ReLU，但在实际使用中目前并没有好的证据证明ELU总是优于ReLU。

十、Noisy Activation Functions

Bengio教授在ICML2016提出了一种激活策略[1]，可用于多种软饱和激活函数，例如sigmoid和tanh。


当激活函数发生饱和时，网络参数还能够在两种动力下继续更新：正则项梯度和噪声梯度。引入适当的噪声能够扩大SGD的参数搜索范围，从而有机会跳出包河区。在激活函数中引入噪声的更早工作可追溯到[5]，但文献[5]的工作并不考虑噪声引入的时间和大小。本篇的特点在于，只在饱和区引入噪声，且噪声量与饱和程度相关（原式与泰勒展开式一次项之差$\delta$）。算法1中g表示sigmoid，用于归一化$\delta$。注意，ReLU的$\delta$恒为0，无法直接加噪声，所以作者把噪声加在了输入上。

CReLU

MPELU

十一、小结

建议用ReLU非线性函数。但是要注意初始化和learning rate的设置，或许可以监控你的网络中死亡的神经元占的比例。如果单元死亡问题困扰你，就试试Leaky ReLU或者Maxout，不要再用sigmoid了。也可以试试tanh，但是其效果应该不如ReLU或者Maxout。

参考资料

[1] Gulcehre, C., et al., Noisy Activation Functions, in ICML 2016. 2016.
[2] Glorot, X. and Y. Bengio. Understanding the difficulty of training deep feedforward neural networks. AISTATS 2010.
[3] LeCun, Y., et al., Backpropagation applied to handwritten zip code recognition. Neural computation, 1989. 1(4): p. 541-551.
[4] Amari, S.-I., Natural gradient works efficiently in learning. Neural computation, 1998. 10(2): p. 251-276.
[5] Nair, V. and G.E. Hinton. Rectified linear units improve Restricted Boltzmann machines. ICML 2010.
[6] Glorot, X., A. Bordes, and Y. Bengio. Deep Sparse Rectifier Neural Networks.AISTATS 2011.
[7] Djork-Arné Clevert, T.U., Sepp Hochreiter. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). ICLR 2016.
[]
[9] Xu, B., et al. Empirical Evaluation of Rectified Activations in Convolutional Network. ICML Deep Learning Workshop 2015.
[10] He, K., et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. ICCV 2015.
[11] He, K. and J. Sun Convolutional Neural Networks at Constrained Time Cost. CVPR 2015.
[12] Maas, A.L., Awni Y. Hannun, and Andrew Y. Ng. Rectifier nonlinearities improve neural network acoustic models. in ICML 2013.
[13] Goodfellow, I.J., et al. Maxout Networks. ICML 2013..