“An outlier is an observation which deviates so much from other observations as to arouse suspicions that it was generated by a different mechanism.” — D. M. Hawkins, Identification of Outliers, Chapman and Hall, 1980.
异常检测 (anomaly detection),或者又被称为“离群点检测” (outlier detection),是机器学习研究领域中跟现实紧密联系、有广泛应用需求的一类问题。但是,什么是异常,并没有标准答案,通常因具体应用场景而异。如果要给一个比较通用的定义,很多文献通常会引用 Hawkins 在文章开头那段话。很多后来者的说法,跟这个定义大同小异。这些定义虽然笼统,但其实暗含了认定“异常”的两个标准或者说假设:
- 1)异常数据跟样本中大多数数据不太一样。
- 2)异常数据在整体数据样本中占比比较小。
为了刻画异常数据的“不一样”,最直接的做法是利用各种统计的、距离的、密度的量化指标去描述数据样本跟其他样本的疏离程度。而 Isolation Forest (Liu et al. 2011) 的想法要巧妙一些,它尝试直接去刻画数据的“疏离”(isolation)程度,而不借助其他量化指标。Isolation Forest 因为简单、高效,在学术界和工业界都有着不错的名声。
一、简介
我们先用一个简单的例子来说明 Isolation Forest 的基本想法。假设现在有一组一维数据(如下图所示),我们要对这组数据进行随机切分,希望可以把点 A 和点 B 单独切分出来。具体的,我们先在最大值和最小值之间随机选择一个值 x,然后按照 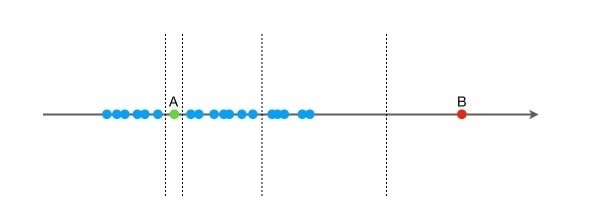
我们把数据从一维扩展到两维。同样的,我们沿着两个坐标轴进行随机切分,尝试把下图中的点A’和点B’分别切分出来。我们先随机选择一个特征维度,在这个特征的最大值和最小值之间随机选择一个值,按照跟特征值的大小关系将数据进行左右切分。然后,在左右两组数据中,我们重复上述步骤,再随机的按某个特征维度的取值把数据进行细分,直到无法细分,即:只剩下一个数据点,或者剩下的数据全部相同。跟先前的例子类似,直观上,点B’跟其他数据点比较疏离,可能只需要很少的几次操作就可以将它细分出来;点A’需要的切分次数可能会更多一些。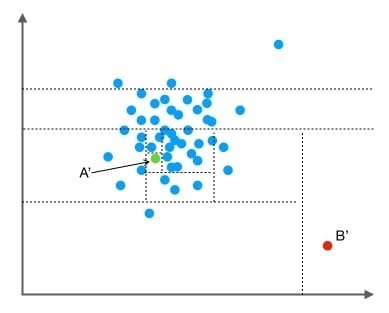
按照先前提到的关于“异常”的两个假设,一般情况下,在上面的例子中,点B和点B’ 由于跟其他数据隔的比较远,会被认为是异常数据,而点A和点A’ 会被认为是正常数据。直观上,异常数据由于跟其他数据点较为疏离,可能需要较少几次切分就可以将它们单独划分出来,而正常数据恰恰相反。这其实正是 Isolation Forest(IF)的核心概念。IF采用二叉树去对数据进行切分,数据点在二叉树中所处的深度反应了该条数据的“疏离”程度。整个算法大致可以分为两步:
- 训练:抽取多个样本,构建多棵二叉树(Isolation Tree,即 iTree);
- 预测:综合多棵二叉树的结果,计算每个数据点的异常分值。
训练:
构建一棵 iTree 时,先从全量数据中抽取一批样本,然后随机选择一个特征作为起始节点,并在该特征的最大值和最小值之间随机选择一个值,将样本中小于该取值的数据划到左分支,大于等于该取值的划到右分支。然后,在左右两个分支数据中,重复上述步骤,直到满足如下条件:
- 1)数据不可再分,即:只包含一条数据,或者全部数据相同。
- 2)二叉树达到限定的最大深度。

预测:
计算数据 x 的异常分值时,先要估算它在每棵 iTree 中的路径长度(也可以叫深度)。具体的,先沿着一棵 iTree,从根节点开始按不同特征的取值从上往下,直到到达某叶子节点。假设 iTree 的训练样本中同样落在 x 所在叶子节点的样本数为 T.size,则数据 x 在这棵 iTree 上的路径长度 h(x),可以用下面这个公式计算:
公式中,$e$表示数据$x$从$iTree$的根节点到叶节点过程中经过的边的数目,$C(T.size)$ 可以认为是一个修正值,它表示在一棵用 $T.size$ 条样本数据构建的二叉树的平均路径长度。一般的,$C(n)$的计算公式如下:
其中,$H(n-1)$可用$ln(n-1)+0.5772156649$估算,这里的常数是欧拉常数。数据 x 最终的异常分值 Score(x) 综合了多棵 iTree 的结果:
公式中,$E(h(x)) $表示数据 x 在多棵 iTree 的路径长度的均值,$\psi$表示单棵 iTree 的训练样本的样本数,$C(\psi)$ 表示用$\psi$条数据构建的二叉树的平均路径长度,它在这里主要用来做归一化。
从异常分值的公式看,如果数据 x 在多棵 iTree 中的平均路径长度越短,得分越接近 1,表明数据 x 越异常;如果数据 x 在多棵 iTree 中的平均路径长度越长,得分越接近 0,表示数据 x 越正常;如果数据 x 在多棵 iTree 中的平均路径长度接近整体均值,则打分会在 0.5 附近。
二、算法特点
在论文中,也比较了其它的常用异常挖掘的算法。比如常用的统计方法,基于分类的方法,和基于聚类的方法,这些传统算法通常是对正常的数据构建一个模型,然后把不符合这个模型的数据,认为是异常数据。而且,这些模型通常为正常数据作优化,而不是为异常数据作优化。而iForest可以显示地找出异常数据,而不用对正常的数据构建模型。
由于异常数据的两个特征(少且不同: few and different):异常数据只占很少量;异常数据特征值和正常数据差别很大。
异常数据的这两个特征,确定了算法的理论基础。因此,构建二叉树型结构的时候,异常数据离根更近,而正常数据离根更远,更深。算法为了效率考虑,也限定了树的深度:ceil(log2(n)),这个值近似于树的平均深度,因为只需要关心那些低于平均高度的数据点,而不需要树进行完全生成。
算法只需要两个参数:树的多少与采样的多少。实验发现,在100颗树的时候,路径的长度就已经覆盖得比较好了,因此选100颗也就够了。采样,是为了更好的将正常数据和异常数据分离开来。有别于其它模型,采样数据越多,反面会降低iForest识别异常数据的能力。因为,通常使用256个样本,这也是scikit-learn实现时默认使用的采样数。
由于算法只需要采样数据256条样本,并且对树的深度也有限制,因此,算法对内存要求很低,且处理速度很快,其时间复杂度也是线性的。
不像其它算法,需要计算距离或者密度来寻找异常数据,iForest算法可以很好的处理高维数据和大数据,并且也可以作为在线预测。假设采样为256条,结点最大为511个,假设一个节点占b字节,共使用t颗树,那么需要的内存只有511tb字节,基本上只需要几M到几十M的内存就够了。数据还显示,预测287,748条数据只花了7.6秒。
另外,iForest既能发现群异常数据,也能发现散点异常数据。同时也能处理训练数据中不包含异常数据的情况。
三、代码示例
|
|
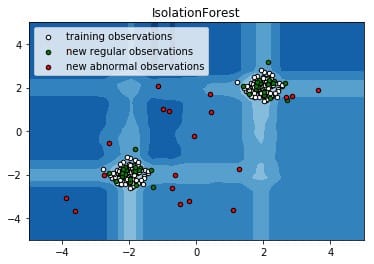
算法基本上不需要配置参数就可以直接使用,通常就以下几个(参数明显比随机森林简单):
- n_estimators: 默认为100,配置iTree树的多少
- max_samples: 默认为265,配置采样大小
- max_features: 默认为全部特征,对高维数据,可以只选取部分特征

