Free Will

数据结构与算法（3）：二叉树

发表于 | 分类于 |

数据结构中有很多树的结构，这里整理了二叉树、二叉查找树、AVL树、红黑树、B树、B+树、trie树的基本概念与操作。

一、二叉树的概念

1.1 树的基本概念

树是一种数据结构，它是由n（n>=1）个有限节点组成一个具有层次关系的集合。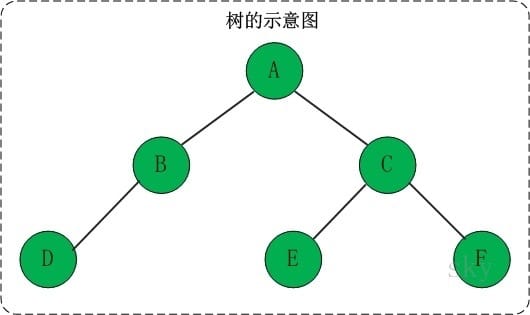

它具有以下特点：

  • 每个节点有零个或多个子节点；
  • 没有父节点的节点称为根节点；
  • 每一个非根节点有且只有一个父节点；
  • 除了根节点外，每个子节点可以分为多个不相交的子树。

若一个结点有子树，那么该结点称为子树根的”双亲”，子树的根是该结点的”孩子”。有相同双亲的结点互为”兄弟”。一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。

  • 结点的度：结点拥有的子树的数目。
  • 叶子：度为零的结点。
  • 分支结点：度不为零的结点。
  • 树的度：树中结点的最大的度。
  • 层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。
  • 树的高度：树中结点的最大层次。
  • 无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。
  • 有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
  • 森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

  • 1.2 二叉树的定义

    二叉树是每个节点最多有两个子树（不存在度大于2的结点）的树结构。二叉树的子树有左右之分，次序不能颠倒。它有5种基本形态：二叉树可以是空集；根可以有空的左子树或右子树；或者左右子树皆为空。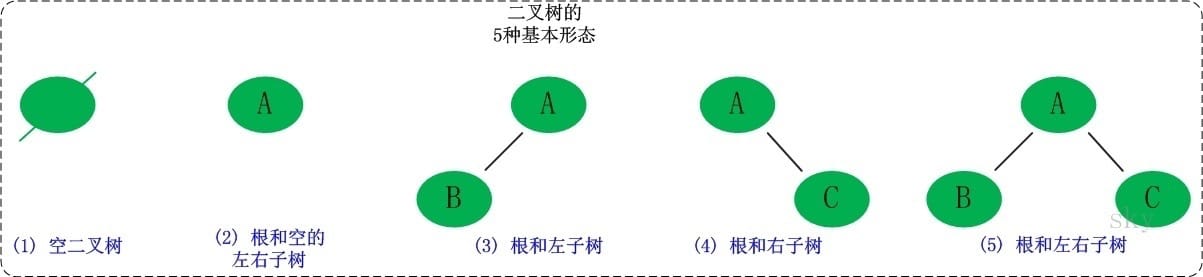

1.3 二叉树的性质

1.3.1 性质一

二叉树的第i层至多有$2^{i-1}$个结点；

证明：下面用”数学归纳法”进行证明。

  • 当$i=1$时，第$i$层的节点数目为$2^{i-1}=2^{0}=1$。因为第1层上只有一个根结点，所以命题成立。
  • 假设当$i>1$，第$i$层的节点数目为$2^{i-1}$。这个是根据(01)推断出来的！
  • 下面根据这个假设，推断出”第$(i+1)$层的节点数目为$2^{i}$”即可。由于二叉树的每个结点至多有两个孩子，故”第$(i+1)$层上的结点数目” 最多是 “第i层的结点数目的2倍”。即，第$(i+1)$层上的结点数目最大值$=2×2^{i-1}=2^{i}$。
  • 故假设成立，原命题得证！

1.3.2 性质二

深度为k的二叉树至多有$2^{k-1}$个结点；

证明：在具有相同深度的二叉树中，当每一层都含有最大结点数时，其树中结点数最多。利用”性质1”可知，深度为k的二叉树的结点数至多为: $2^0+2^1+…+2^{k-1}=2^k-1$故原命题得证！

1.3.3 性质三

包含n个结点的二叉树的高度至少为$log_2 (n+1)$；

证明：根据”性质2”可知，高度为h的二叉树最多有2{h}–1个结点。反之，对于包含n个节点的二叉树的高度至少为$log_2(n+1)$。

1.3.4 性质四

对任何一颗二叉树T，如果其终端结点数为$n_0$，度为2的结点数为$n_2$，则$n_0=n_2+1$

证明：因为二叉树中所有结点的度数均不大于2，所以结点总数(记为n)=”0度结点数$(n_0)$” + “1度结点数$(n_1)$” + “2度结点数$(n_2)$”。由此，得到等式一。(等式一) $n=n_0+n_1+n_2$

另一方面，0度结点没有孩子，1度结点有一个孩子，2度结点有两个孩子，故二叉树中孩子结点总数是：$n_1+2n_2$。

此外，只有根不是任何结点的孩子。故二叉树中的结点总数又可表示为等式二。 (等式二) $n=n1+2n_2+1$

由(等式一)和(等式二)计算得到：n0=n2+1。原命题得证！

1.4 满二叉树和完全二叉树

1.4.1 满二叉树

满二叉树的定义：
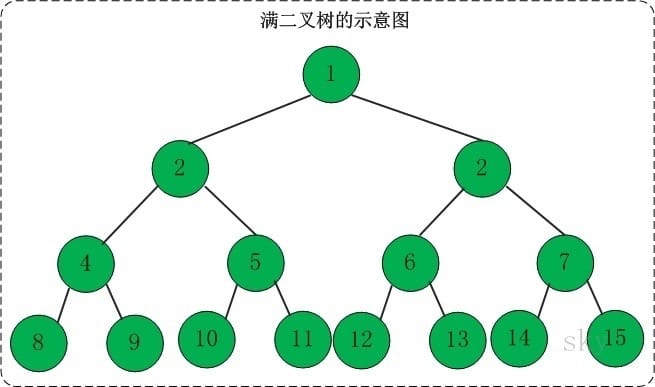
除最后一层无任何子节点外，每一层上的所有结点都有两个子结点。也可以这样理解，除叶子结点外的所有结点均有两个子结点。节点数达到最大值，所有叶子结点必须在同一层上。

满二叉树的性质：

  1. 一棵树的深度为h，最大层数为k，深度与最大层数相同，k=h；
  2. 叶子数为$2^h$
  3. 第k层的结点数是：$2^{k-1}$；
  4. 总结点数是$2^k-1$，且总节点数一定是奇数。

1.4.2 完全二叉树

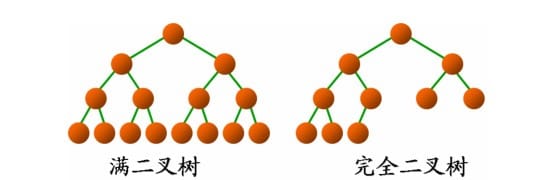
定义：一颗二叉树中，只有最小面两层结点的度可以小于2，并且最下一层的叶结点集中在靠左的若干位置上。这样的二叉树称为完全二叉树。

特点：叶子结点只能出现在最下层和次下层，且最小层的叶子结点集中在树的左部。显然，一颗满二叉树必定是一颗完全二叉树，而完全二叉树未必是满二叉树。

注意：完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、Dijkstra算法、Prim算法等都要用堆才能优化，二叉排序树的效率也要借助平衡树来提高，而平衡性基于完全二叉树。

2019-05-17-165559-1.jpg

二、二叉树的遍历

【提问】

  1. 请分别写出并解释二叉树的先序、中序、后续遍历的递归与非递归版本
  2. 给定二叉树的先序跟后序遍历，能不能将二叉树重建：不能，因为先序为父节点-左节点-右节点，后序为左节点-右节点-父节点，两者的拓扑序列是一样的，所以无法建立；如果换成一棵二叉搜索树的后续能不能建立：可以，因为只要将遍历结果排序就可以得到中序结果。

这块内容讨论二叉树的常见遍历方式的代码（java）实现，包括前序（preorder）、中序（inorder）、后序（postorder）、层序（levelorder），进一步考虑递归和非递归的实现方式。
递归的实现方法相对简单，但由于递归的执行方式每次都会产生一个新的方法调用栈，如果递归层级较深，会造成较大的内存开销，相比之下，非递归的方式则可以避免这个问题。递归遍历容易实现，非递归则没那么简单，非递归调用本质上是通过维护一个栈，模拟递归调用的方法调用栈的行为。

在此之前，先简单定义节点的数据结构：

二叉树节点最多只有两个儿子，并保存一个节点的值，为了实验的方便，假定它为 int。同时，我们直接使用 Java 的 System.out.print 方法来输出节点值，以显示遍历结果。

1
2
3
4
5
6
7
8
9
10
11
class Node{  
    public int value;  
    public Node left;  
    public Node right;  
    public Node(int v){  
        this.value=v;  
        this.left=null;  
        this.right=null;  
    }  
      
}

2.1 前序遍历

2.1.1 递归实现

递归实现很简单，在每次访问到某个节点时，先输出节点值，然后再依次递归的对左儿子、右儿子调用遍历的方法。代码如下

java

1
2
3
4
5
6
7
public void preOrder(Node root){
    if(root!=null){
        System.out.print(root.value);
        preOrder(root.left);
        preOrder(root.right);
    }
}

2.1.2 非递归实现

利用栈实现循环先序遍历二叉树，维护一个栈，将根节点入栈，只要栈不为空，出栈并访问，接着依次将访问节点的右节点、左节点入栈。这种方式是对先序遍历的一种特殊实现，简洁明了，但是不具备很好地扩展性，在中序和后序方式中不适用。

1
2
3
4
5
6
7
8
9
10
11
public void preOrder(Node root){
    if(root==null)return;
    Stack<Node> stack = new Stack<Node>();
    stack.push(root);
    while(!stack.isEmpty){
        Node temp = stack.pop();
        System.out.print(temp.value);
        if(temp.right!=null)stack.push(temp.right);
        if(temp.left!=null)stack.push(temp.left);
    }
}

还有一种方式就是利用栈模拟递归过程实现循环先序遍历二叉树。这种方式具备扩展性，它模拟了递归的过程，将左子树不断的压入栈，直到null，然后处理栈顶节点的右子树。

java

1
2
3
4
5
6
7
8
9
10
11
12
13
public void preOrder(Node root){
    if(root==null)return;
    Stack<Node> s = new Stack<Node>();
    while(root!=null||!s.isEmtpy()){
        while(root!=null){
            System.out.print(root.value);、//先访问
            s.push(root);//再入栈
            root = root.left;
        }
        root = s.pop();
        root = root.right;//如果是null，出栈并处理右子树
    }
}

2.2 中序遍历

2.2.1 递归实现

1
2
3
4
5
6
7
public void inOrder(Node root){
    if(root!=null){
        preOrder(root.left);
        System.out.print(root.value);
        preOrder(root.right);
    }
}

2.2.2 非递归实现

利用栈模拟递归过程实现循环中序遍历二叉树。跟前序遍历的非递归实现方法二很类似。唯一的不同是访问当前节点的时机：前序遍历在入栈前访问，而中序遍历在出栈后访问。

java

1
2
3
4
5
6
7
8
9
10
11
12
13
public void inOrder(Node root){
    if(root==null)return;
    Stack<Node> s = Stack<Node>();
    while(root!=null||s.isEmpty()){
        while(root!=null){
            s.push(root);
            root=root.left;
        }
        root = s.pop(root);
        System.out.print(root.value);
        root = root.right;
    }
}

2.3 后序遍历

2.3.1 递归实现

1
2
3
4
5
6
7
public void inOrder(Node root){
    if(root!=null){
        preOrder(root.left);
        preOrder(root.right);
        System.out.print(root.value);
    }
}

2.3.2 非递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void postOrder(Node root){
    if(root==null)return;
    Stack<Node> s1 = new Stack<Node>();
    Stack<Node> s2 = new Stack<Node>();
    Node node = root;
    s1.push(node);
    while(s1!=null){//这个while循环的功能是找出后序遍历的逆序，存在s2里面
        node = s1.pop();
        if(node.left!=null) s1.push(node.left);
        if(node.right!=null)s1.push(node.right);
        s2.push(node);     
    }
    while(s2!=null){//将s2中的元素出栈，即为后序遍历次序
        node = s2.pop();
        System.out.print(node.value);
    }
}

2.4 层序遍历

1
2
3
4
5
6
7
8
9
10
11
public static void levelTravel(Node root){  
        if(root==null)return;  
        Queue<Node> q=new LinkedList<Node>();  
        q.add(root);  
        while(!q.isEmpty()){  
            Node temp =  q.poll();  
            System.out.println(temp.value);  
            if(temp.left!=null)q.add(temp.left);  
            if(temp.right!=null)q.add(temp.right);  
        }  
    }

总结一下：树的遍历主要有两种，一种是深度优先遍历，像前序、中序、后序；另一种是广度优先遍历，像层次遍历。在树结构中两者的区别还不是非常明显，但从树扩展到有向图，到无向图的时候，深度优先搜索和广度优先搜索的效率和作用还是有很大不同的。 深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。



应统联盟


连接十万名应统专业同学


阿药算法


打通算法面试任督二脉