一、定义
二叉排序树(Binary Sort Tree)又称为二叉查找树(Binary Search Tree)、二叉搜索树。它是特殊的二叉树:对于二叉树,假设x为二叉树中的任意一个结点,x节点包含关键字key,节点x的$key$值记为$key[x]$。如果y是x的左子树中的一个结点,则$key[y]<= key[x]$;如果y是x的右子树的一个结点,则$key[y] >= key[x]$。那么,这棵树就是二叉查找树。
二叉查找树是先对待查找的数据进行生成树,确保树的左分支的值小于右分支的值,然后再就行和每个节点的父节点比较大小,查找最合适的范围。这个算法的效率查找效率很高,但是如果使用这种查找方法要首先创建树。
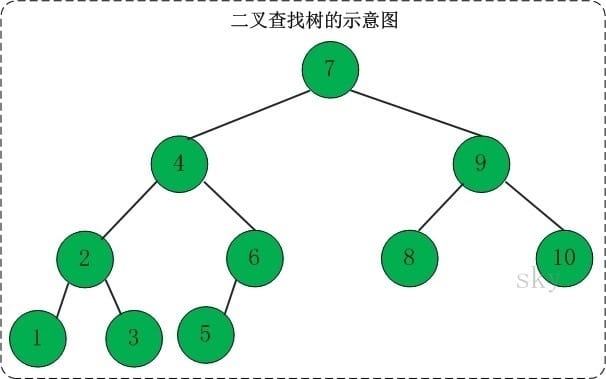
它或者是一颗空树,或者是具有下列性质的二叉树:
- 若任意节点的左子树不为空,则左子树上的所有节点的值均小于它的根结点的值;
- 若任意节点的右子树不为空,则左子树上所有节点的值均小于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树。
- 没有键值相等的节点。
二叉查找树的性质:对二叉查找树进行中序遍历,即可得到有序的数列。
构造一颗二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除关键字的速度。不管怎么说,在一个有序数据集上的查找,速度总是要快于无序的数据集的,而二叉排序树这样的非线性结构,也有利于插入和排序的实现。
二叉查找树的高度决定了二叉查找树的查找效率。
二、查找、插入与删除
2.1 查找
在二叉查找树中查找x的过程如下:
- 若二叉树是空树,则查找失败。
- 若x等于根结点的数据,则查找成功,否则。
- 若x小于根结点的数据,则递归查找其左子树,否则。
- 递归查找其右子树。
复杂度分析,它和二分查找一样,插入和查找的时间复杂度均为O(logn),但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡(比如,我们查找上图(b)中的“93”,我们需要进行n次查找操作)。我们追求的是在最坏的情况下仍然有较好的时间复杂度,这就是平衡查找树设计的初衷。
根据上述的步骤,写出其查找操作的代码:
|
|
2.2 插入
插入:从根结点开始逐个与关键字进行对比,小了去左边,大了去右边,碰到子树为空的情况就将新的节点连接。二叉查找树的插入过程如下:
- 1) 若当前的二叉查找树为空,则插入的元素为根节点;
- 2) 若插入的元素值小于根节点值,则将元素插入到左子树中;
- 3) 若插入的元素值不小于根节点值,则将元素插入到右子树中。
|
|
2.3 删除
如果要删除的节点是叶子,直接删;如果只有左子树或只有右子树,则删除节点后,将子树连接到父节点即可;如果同时有左右子树,则可以将二叉排序树进行中序遍历,取将要被删除的节点的前驱或者后继节点替代这个被删除的节点的位置。
二叉查找树的删除,分三种情况进行处理:
- 1) p为叶子节点,直接删除该节点,再修改其父节点的指针(注意分是根节点和不是根节点),如图a;
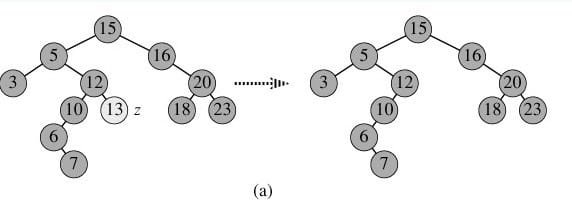
- p为单支节点(即只有左子树或右子树)。让p的子树与p的父亲节点相连,删除p即可(注意分是根节点和不是根节点),如图b;
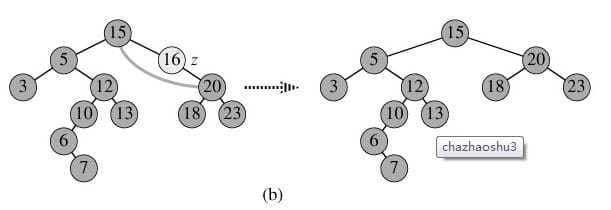
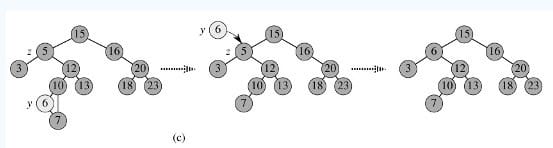
- p的左子树和右子树均不空。找到p的后继y,因为y一定没有左子树,所以可以删除y,并让y的父亲节点成为y的右子树的父亲节点,并用y的值代替p的值;或者方法二是找到p的前驱x,x一定没有右子树,所以可以删除x,并让x的父亲节点成为y的左子树的父亲节点。如图c。
|
|
2.4 总结
二叉排序树总结:
- 二叉排序树以链式进行存储,保持了链式结构在插入和删除操作上的优点。
- 在极端情况下,查询次数为1,但最大操作次数不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序书的形状,也就引申除了后面的平衡二叉树。
- 给定一个元素集合,可以构造不同的二叉排序树,当它同时是一个完全二叉树的时候,查找的时间复杂度为$O(log(n))$,近似于二分查找。
- 当出现最极端的斜树时,时间复杂度为$O(n)$,等同于顺序查找,效果最差。
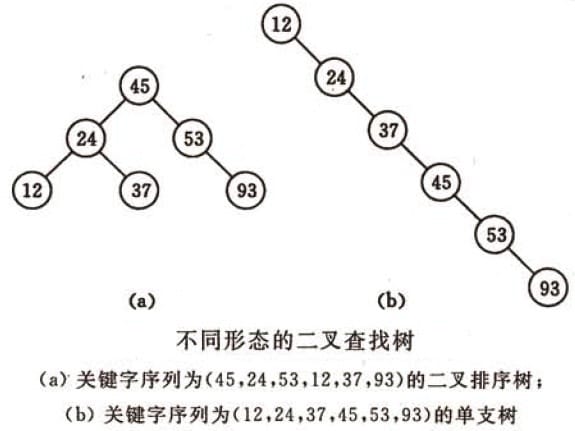
下图为二叉树查找和顺序查找以及二分查找性能的对比图:
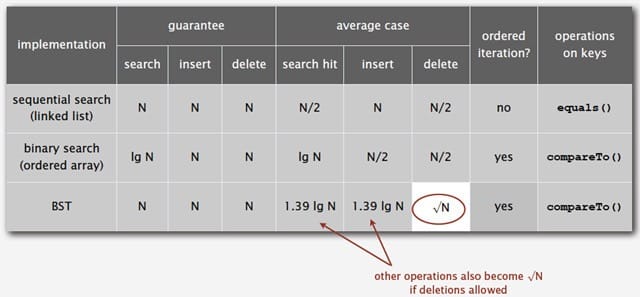
基于二叉查找树进行优化,进而可以得到其他的树表查找算法,比如平衡树、红黑树等高效算法。

