机器学习算法系列（28）：L1、L2正则化

之前讨论了机器学习中的偏差-方差权衡。机器学习里的损失函数（代价函数）可以用来描述模型与真模型（ground truth）之间的差距，因此可以解决“偏差”的问题。但是仅有损失函数，我们无法解决方差的问题，因而会有过拟合风险。

这次我们讨论损失函数的反面——正则项，看看L1正则项和L2正则项是如何使机器学习模型避免过拟合的。

我们希望选择或学习一个合适的模型。若在空间中存在“真模型”，那我们所选择的模型要与真模型的参数个数相同，所选择的模型的参数向量与真模型的参数向量相近。

过拟合指的是我们以为追求提高模型对训练数据的预测能力，所选模型的复杂度往往会比真模型更高。即学习时选择的模型所包含的参数过多，以致于出现这一模型对已知数据预测得很好，但对未知数据预测得很差的现象。

一、从经验风险最小化到结构经验最小化

经验风险最小化（empirical risk minimization）认为经验风险最小的模型是最优的模型，即求解最优化问题：

$\underset{f\in\mathscr{F}}{\min}\frac{1}{N}\sum_{i=1}^N{L\left(y_i,f\left(x_i\right)\right)}$

当样本容量足够大的时候，经验风险最小化学习效果良好。比如极大似然估计，当模型是条件概率分布，损失函数是对数损失函数时，经验风险最小化就等价于极大似然估计。

但是当样本容量很小时，经验风险最小化学习会产生过拟合（over-fitting）的现象。这就引出了结构风险最小化，它等价于正则化（regularization）。结构风险在经验风险上加上表示模型复杂度的正则化项（regularizer）或罚项（penalty term），它的定义为：

$R_{srm}\left(f\right)=\frac{1}{N}\sum_{i=1}^N{L\left(y_i,f\left(x_i\right)\right)}+\lambda J\left(f\right)$

其中$J(f)$为模型的复杂度，模型$f$越复杂，复杂度$J(f)$就越大；反之，模型越简单，复杂度$J(f)$就越小，即复杂度表示了对复杂模型的惩罚。$\lambda≥0$是系数，用以权衡经验风险和模型复杂度。结构风险小需要经验风险和模型复杂度同时小。结构风险小的模型往往对训练数据以及未知的测试数据都有较好的预测。比如贝叶斯估计中的最大后验概率估计就是结构风险最小化的一个例子。当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时，结构风险最小化就等价于最大后验概率估计。
结构风险最小化的策略认为结构风险最小的模型是最优的模型，求解最优模型即求解最优化问题：

$\min_{f\in\mathscr{F}}\frac{1}{N}\sum_{i=1}^N{L\left(y_i,f\left(x_i\right)\right)}+\lambda J\left(f\right)$

这样，监督学习问题变成了经验风险或结构风险函数的最优化问题。

其中正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或罚项。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大。比如，正则化项可以是模型参数向量的范数。它的一般形式如下：

$\min_{f\in\mathscr{F}}\frac{1}{N}\sum_{i=1}^N{L\left(y_i,f\left(x_i\right)\right)}+\lambda J\left(f\right)$

第一项是经验风险，第二项是正则化项，$\lambda≥0$为调整两者之间关系的系数。

二、范数与正则项

在线性代数、函数分析等数学分支中，范数（Norm）是一个函数，其赋予某个向量空间（或矩阵）中的每个向量以长度或大小。对于零向量，另其长度为零。直观的说，向量或矩阵的范数越大，则我们可以说这个向量或矩阵也就越大。有时范数有很多更为常见的叫法，如绝对值其实便是一维向量空间中实数或复数的范数，而Euclidean距离也是一种范数。

范数满足通常意义上长度的三个基本性质：

非负性：$||\vec{x}||≥0$
齐次性：$||c·\vec{x}||=|c|||\vec{x}||$
三角不等式：$||\vec{x}+\vec{y}||≤||\vec{x}||+||\vec{y}||$

在这里，我们需要关注的最主要是范数的「非负性」。我们刚才讲，损失函数通常是一个有下确界的函数。而这个性质保证了我们可以对损失函数做最优化求解。如果我们要保证目标函数依然可以做最优化求解，那么我们就必须让正则项也有一个下界。非负性无疑提供了这样的下界，而且它是一个下确界——由齐次性保证（当 c=0 时）。

因此，我们说，范数的性质使得它天然地适合作为机器学习的正则项。而范数需要的向量，则是机器学习的学习目标——参数向量。

范数的一般化定义：设$p≥1$的实数，$p-norm$定义为：

$||x||_p:=(\sum_{i=1}^n|x_i|^p)^{\frac{1}{p}} \ \ \ \ （1）$

机器学习中有几个常用的范数，分别是：

$L_1-$范数：$||x⃗ ||=∑^d_{i=1}| x_i|$;
$L_2-$范数：$||x⃗ ||_2=(∑^d_{i=1}x^2_i)^{1/2}$；
$L_p-$范数：$||x||_p=(\sum_{i=1}^n|x_i|^p)^{\frac{1}{p}}$
$L_∞-$范数：$||x⃗ ||_∞=lim_{p→+∞}(∑^d_{i=1}x^p_i)^{1/p}$。

当p=1时，我们称之为taxicab Norm，也叫Manhattan Norm。其来源是曼哈顿的出租车司机在四四方方的曼哈顿街道中从一点到另一点所需要走过的距离。也即我们所要讨论的l1范数。其表示某个向量中所有元素绝对值的和。

而当p=2时，则是我们最为常见的Euclidean norm。也称为Euclidean distance。也即我们要讨论的l2范数。

而当p=0时，因其不再满足三角不等性，严格的说此时p已不算是范数了，但很多人仍然称之为l0范数。这三个范数有很多非常有意思的特征，尤其是在机器学习中的正则化（Regularization）以及稀疏编码（Sparse Coding）有非常有趣的应用。

下图给出了一个Lp球的形状随着P的减少的可视化图。

在机器学习中，如果使用了$||\vec{w}||_p作为正则项$，则我们说，该机器学习任务引入了$L_p-$正则项。

2.1 $L_0$与$L_1-$正则项（LASSO regularizer）

在机器学习里，最简单的学习算法可能是所谓的线性回归模型

$F(x⃗ ;w⃗ ,b)=∑_{i=1}^nw_i⋅x_i+b$

我们考虑这样一种普遍的情况，即：预测目标背后的真是规律，可能只和某几个维度的特征有关；而其它维度的特征，要不然作用非常小，要不然纯粹是噪声。在这种情况下，除了这几个维度的特征对应的参数之外，其它维度的参数应该为零。若不然，则当其它维度的特征存在噪音时，模型的行为会发生预期之外的变化，导致过拟合。

于是，我们得到了避免过拟合的第一个思路：使尽可能多的参数为零。为此，最直观地我们可以引入$L_0$-范数。令

$Ω(F(x⃗ ;w⃗ ))\overset{def}=ℓ_0\frac{∥w⃗ ∥_0}{n},ℓ_0>0$

这意味着，我们希望绝大多数$\vec{w}$的分量为零。

通过引入 $L_0-$正则项，我们实际上引入了一种「惩罚」机制，即：若要增加模型复杂度以加强模型的表达能力降低损失函数，则每次使得一个参数非零，则引入 $ℓ_0$ 的惩罚系数。也就是说，如果使得一个参数非零得到的收益（损失函数上的收益）不足 $ℓ_0$；那么增加这样的复杂度是得不偿失的。

通过引入$L_0-$正则项，我们可以使模型稀疏化且易于解释，并且在某种意义上实现了「特征选择」。这看起来很美好，但是 $L_0-$正则项也有绕不过去坎：

非连续
非凸
不可求导

因此，$L_0$正则项虽好，但是求解这样的最优化问题，难以在多项式时间内找到有效解（NP-Hard 问题）。于是，我们转而考虑 L0L0-范数最紧的凸放松（tightest convex relaxation）：L1-范数。令

$Ω(F(x⃗ ;w⃗ ))\overset{def}{=}ℓ_1\frac{∥w⃗ ∥_1}{n},ℓ_1>0$

我们来看一下参数更新的过程，有哪些变化。考虑目标函数

$Obj(F)=L(F)+γ⋅ℓ_1\frac{∥w⃗ ∥_1}{n}$

对参数$w_i$求偏导数

$\frac{∂Obj}{∂w_i}=\frac{∂L}{∂w_i}+\frac{γℓ_1}{n}sgn(w_i)$

因此参数更新的过程为

$w_i→w′_i\overset{def}{=}w_i−η\frac{∂L}{∂w_i}−η\frac{γℓ_1}{n}sgn(w_i)$

因为$η\frac{γℓ_1}{n}>0$所以多出的项$η\frac{γℓ_1}{n}sgn(w_i)$使得$w_i→0$，实现稀疏化。

2.2 $L_2$正则项（Ridge Regularizer）

让我们回过头，考虑多项式模型，它的一般形式为：

$F=∑_{i=1}^nw_i⋅x^i+b$

我们注意到，当多项式模型过拟合时，函数曲线倾向于靠近噪声点。这意味着，函数曲线会在噪声点之间来回扭曲跳跃。这也就是说，在某些局部，函数曲线的切线斜率会非常高（函数导数的绝对值非常大）。对于多项式模型来说，函数导数的绝对值，实际上就是多项式系数的一个线性加和。这也就是说，过拟合的多项式模型，它的参数的绝对值会非常大（至少某几个参数分量的绝对值非常大）。因此，如果我们有办法使得这些参数的值，比较稠密均匀地集中在0附近，就能有效地避免过拟合。

于是我们引入$L_2-$正则项，令

$Ω(F(x⃗ ;w⃗ ))\overset{def}=ℓ_2\frac{∥w⃗ ∥_2 }{2n},ℓ_2>0$

因此有目标函数

$Obj(F)=L(F)+γ⋅ℓ_2\frac{∥w⃗ ∥_2 }{2n}$

对参数$w_i$求偏导数，有

$\frac{∂Obj}{∂w_i}=\frac{∂L}{∂w_i}+\frac{γℓ_2}{n}w_i$

再有参数更新

$w_i→w′_i\overset{def}{=}w_i−η\frac{∂L}{∂w_i}−η\frac{γℓ_2}{n}w_i=(1−η\frac{γℓ_2}n)w_i−η\frac{∂L}{∂w_i}$

考虑到$η\frac{γℓ_2}{n}>0$，因此，引入$L_2-$正则项之后，相当于衰减了（decay）参数的权重，使参数趋近于0。

2.3 $L_1-$正则项与$L_2-$正则项的区别

现在，我们考虑这样一个问题：为什么使用$L-1-$正则项，会倾向于使得参数稀疏化；而使用$L_2-$正则项，会倾向于使得参数稠密地接近于0？

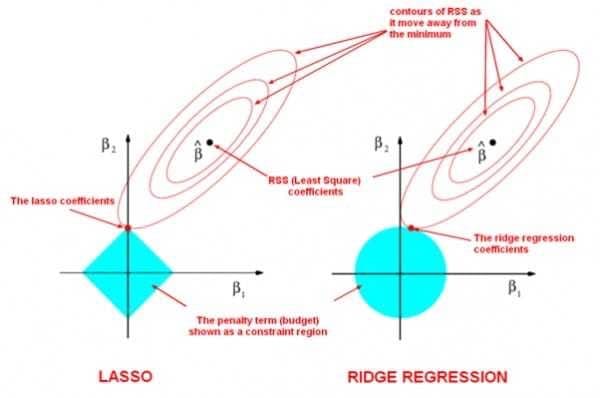
这里引用一张来自周志华老师的著作，《机器学习》（西瓜书）里的插图，尝试解释这个问题。

为了简便起见，我们只考虑模型有两个参数$w_1$和$w_2$的情形。

在图中，我们有三组等值线，位于同一条等值线上的$w_1$与$w_2$映射到相同的平方损失项、$L_1-$范数和$L_2-$范数。并且，对于三组等值线来说，当$(w_1,w_2)$沿着等值线法线方向，向外扩张，则对应的值增大；反之，若沿着法线向内收缩，则对应的值减小。

因此，对于目标函数$Obj(F)$来说，实际上是要在正则项的等值线与损失函数的等值线中寻找一个交点，使得二者的和最小。

对于$L_1-$正则项来说，因为$L_1-$正则项是一组菱形，这些交点容易落在坐标轴上。因此，另一个参数的值在这个交点上就是0，从而实现了稀疏化。

对于 $L_2-$正则项来说，因为 $L_2-$正则项的等值线是一组圆形。所以，这些交点可能落在整个平面的任意位置。所以它不能实现「稀疏化」。但是，另一方面，由于 $(w_1,w_2)$ 落在圆上，所以它们的值会比较接近。这就是为什么 $L_2-$正则项可以使得参数在零附近稠密而平滑。

三、贝叶斯先验

从贝叶斯的角度来看，正则化等价于对模型参数引入先验分布。

3.1 Linear Regression

我们先看下最原始的线性回归：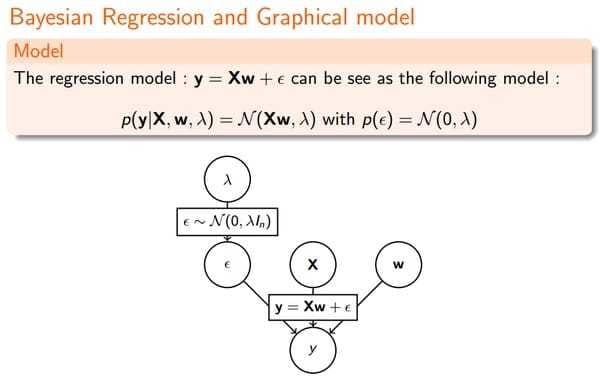

$\begin{align*} & p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(\epsilon^{(i)})^2}{2\delta^2} \right)\\ \Rightarrow & p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right) \end{align*}$

由最大似然估计（MLE）：

$\begin{align*} L(w) & = p(\vec{y}|X;w)\\ & = \prod_{i=1}^{m} p(y^{(i)}|x^{(i)};\theta)\\ & = \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right) \end{align*}$

取对数：

$\begin{align*} l(w) & = \log L(w)\\ & =\log \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})}{2\delta^2} \right)\\ & = \sum_{i=1}^{m} \log \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right)\\ & = m \log \frac{1}{\sqrt{2\pi}\delta} - \frac{1}{\delta^2}\cdot \frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - w^Tx^{(i)})^2 \end{align*}$

即

$w_{MLE} = \arg \underset{w}{\min} \sum_{i=1}^{m} (y^{(i)} - w^Tx^{(i)})^2$

这就导出了我们最原始的$least-squares$损失函数，但这是在我们对参数$w$没有加入任何先验分布的情况下。在数据维度很高的情况下，我们的模型参数很多，模型复杂度高，容易发生过拟合。

比如我们常说的 “small n, large p problem”。（我们一般用 n 表示数据点的个数，用 p 表示变量的个数，即数据维度。当的时候，不做任何其他假设或者限制的话，学习问题基本上是没法进行的。因为如果用上所有变量的话， p 越大，通常会导致模型越复杂，但是反过来 n 又很小，于是就会出现很严重的 overfitting 问题。Linear regression一般只对low dimension适用，比如n=50, p=5，而且这五个变量还不存在multicolinearity.

这个时候，我们可以对参数$w$引入先验分布，降低模型复杂度。

3.2 Ridge Regression

Ridge Regression的提出就是为了解决multicolinearity的，加一个L2 penalty term也是因为算起来方便。然而它并不能shrink parameters to 0.所以没法做variable selection。

我们对参数 w 引入协方差为 $\alpha$ 的零均值高斯先验。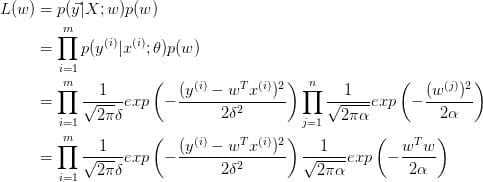

取对数：

等价于：

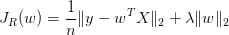
这不就是Ridge Regression吗？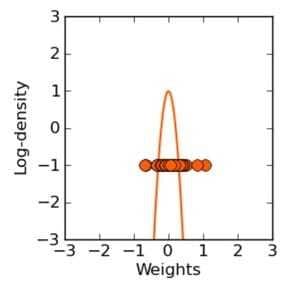

看我们得到的参数，在零附近是不是很密集，老实说 ridge regression 并不具有产生稀疏解的能力，也就是说参数并不会真出现很多零。假设我们的预测结果与两个特征相关，L2正则倾向于综合两者的影响，给影响大的特征赋予高的权重；而L1正则倾向于选择影响较大的参数，而舍弃掉影响较小的那个。实际应用中 L2正则表现往往会优于 L1正则，但 L1正则会大大降低我们的计算量。

Typically ridge or ℓ2 penalties are much better for minimizing prediction error rather than ℓ1 penalties. The reason for this is that when two predictors are highly correlated, ℓ1 regularizer will simply pick one of the two predictors. In contrast, the ℓ2 regularizer will keep both of them and jointly shrink the corresponding coefficients a little bit. Thus, while the ℓ1 penalty can certainly reduce overfitting, you may also experience a loss in predictive power.

那现在我们知道了，对参数引入高斯先验等价于L2正则化。

3.3 LASSO

LASSO是针对Ridge Regression的没法做variable selection的问题提出来的，L1 penalty虽然算起来麻烦，没有解析解，但是可以把某些系数shrink到0。

在Ridge Regression中，我们对 w 引入了高斯分布，那么拉普拉斯分布(Laplace distribution)呢？

注：LASSO - least absolute shrinkage and selection operator.

我们看下拉普拉斯分布长啥样：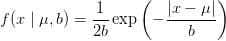

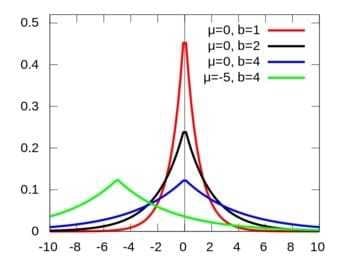
关于拉普拉斯和正态分布的渊源，大家可以参见正态分布的前世今生。
重复之前的推导过程我们很容易得到：

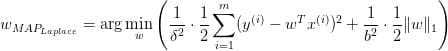
该问题通常被称为 LASSO (least absolute shrinkage and selection operator) 。LASSO 仍然是一个 convex optimization 问题，不具有解析解。它的优良性质是能产生稀疏性，导致 w 中许多项变成零。

再次总结下，对参数引入拉普拉斯先验等价于 L1正则化。

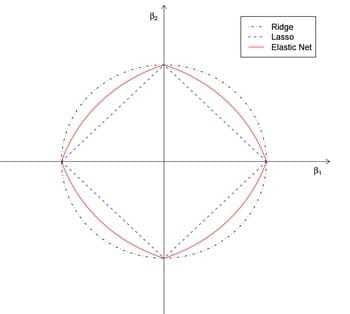
3.4 Elastic Net

然而LASSO虽然可以做variable selection，但是不consistent啊，而且当n很小时至多只能选出n个变量；而且不能做group selection。

可能有同学会想，既然 L1和 L2正则各自都有自己的优势，那我们能不能将他们 combine 起来？

于是有了在L1和L2 penalty之间做个权重就是elastic net

因为lasso在解决之前提到的“small n, large p problem”存在一定缺陷。

得到结果：

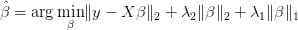
此外针对不consistent有了adaptive lasso，针对不能做group selection有了group lasso, 在graphical models里有了graphical lasso。然后有人说unbiasedness, sparsity and continuity这三条都满足多好，于是有了MCP和SCAD同时满足这三条性质。还有很多penalized regression的方法。