Free Will

数据结构与算法（12）：排序

发表于 | 分类于 |

经典排序算法在面试中占有很大的比重，也是基础，在这里整理并用Java实现了几大经典排序算法，包括冒泡排序、插入排序、选择排序、希尔排序、归并排序、快速排序、堆排序、同排序。我们默认将一个无序数列排序成由小到大。

一、冒泡排序（Bubble Sort）

1.1 思想

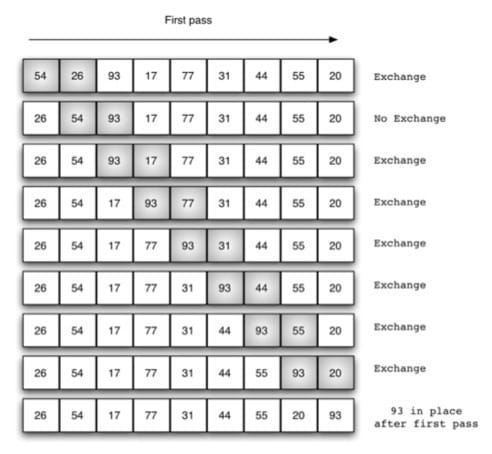
冒泡排序(bubble sort)：每个回合都从第一个元素开始和它后面的元素比较，如果比它后面的元素更大的话就交换，一直重复，直到这个元素到了它能到达的位置。每次遍历都将剩下的元素中最大的那个放到了序列的“最后”(除去了前面已经排好的那些元素)。注意检测是否已经完成了排序，如果已完成就可以退出了。

2019-05-17-164353.jpg

1.2 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class Demo{
	public static void BubbleSort(int[] arr){
	    int temp = 0;
	    for (int i = arr.length - 1; i > 0; --i) { // 每次需要排序的长度
	        for (int j = 0; j < i; ++j) { // 从第一个元素到第i个元素
	            if (arr[j] > arr[j + 1]) {
	                temp = arr[j];
	                arr[j] = arr[j + 1];
	                arr[j + 1] = temp;
	            }
	        }//loop j
	    }//loop i
	}// method bubbleSort
	public static void main(String[] args){
        int[] arr = {10,30,20,60,40,50};
        Demo.BubbleSort(arr);
        for(int i:arr){
            System.out.print(i+",");
        }
    }
}

1.3 时空复杂度

冒泡排序的关键字比较次数与数据元素的初始状态无关。第一趟的比较次数为n-1，第i趟的比较次数为n-i，第n-1趟（最后一趟）的比较次数为1，因此冒泡排序总的比较次数为$n(n-1)/2$

冒泡排序的数据元素移动次数与序列的初始状态有关。在最好的情况下，移动次数为0次；在最坏的情况下，移动次数为$n(n-1)/2$

冒泡排序的时间复杂度为$O(n^2)$。冒泡排序不需要辅助存储单元，其空间复杂度为$O(1)$。如果关键字相等，则冒泡排序不交换数据元素，他是一种稳定的排序方法。

时间复杂度：最好$O(n)$；最坏$O(n^2)$；平均$O(n^2)$
空间复杂度：$O(1)$
稳定性：稳定

二、选择排序（Selection Sort）

2.1 思想

每个回合都选择出剩下的元素中最大的那个，选择的方法是首先默认第一元素是最大的，如果后面的元素比它大的话，那就更新剩下的最大的元素值，找到剩下元素中最大的之后将它放入到合适的位置就行了。和冒泡排序类似，只是找剩下的元素中最大的方式不同而已。

2019-05-17-164402.jpg

2.2 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Demo{
	public static void selectionSort(int[] arr) {
        int temp, min = 0;
        for (int index = 0; index < arr.length - 1; ++index) {
            min = index;
            // 循环查找最小值
            for (int j = index + 1; j < arr.length; ++j) {
                if (arr[min] > arr[j]) {
                    min = j;
                }
            }
            if (min != index) {
                temp = arr[index];
                arr[index] = arr[min];
                arr[min] = temp;
            }
        }
    }
	public static void main(String[] args){
        int[] arr = {10,30,20,60,40,50};
        Demo.selectionSort(arr);
        for(int i:arr){
            System.out.print(i+",");
        }
    }
}

2.3 时空复杂度

对具有$n$个数据元素的序列进行排序时，选择排序需要进行$n-1$趟选择。进行第$i$趟选择时，后面已经有$i-1$个数据元素排好序，第$i$趟从剩下的$n-i+1$个数据元素中选择一个关键字最大的数据元素，并将它与第$i$个数据元素交换，这样即可使后面的$i$个数据元素排好序。

选择排序的关键字比较次数与序列的初始状态无关。对n个数据元素进行排序时，第一趟的比较次数为$n-1$，第$i$趟的比较次数是$n-1$次，第$n-1$趟（最后一趟）的比较次数是1次。因此，总的比较次数为$n(n-1)/2$

选择排序每一趟都可能移动一次数据元素，其总的移动次数与序列的初始状态有关。当序列已经排好序时，元素的移动次数为0。当每一趟都需要移动数据元素时，总的移动次数为$n-1$

选择排序的时间复杂度为$O(n^2)$。选择排序不需要辅助的存储单元，其空间复杂度为$O(1)$。选择排序在排序过程中需要在不相邻的数据元素之间进行交换，它是一种不稳定的排序方法。

时间复杂度：$O(n^2)$
空间复杂度：$O(1)$
稳定性：不稳定

三、插入排序（Insertion Sort）

3.1 思想

对具有$n$个数据元素的序列进行排序时，插入排序需要进行$n-1$趟插入。进行第$j（1≤j≤n-1）$趟插入时，前面已经有$j$个元素排好序了，第$j$趟将$a_{j+1}$插入到已经排好序的序列中，这样即可使前面的$j+1$个数据排好序。

3.2 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Demo{
	public static void insertionSort(int[] arr){
	    for (int i=1; i<arr.length; ++i){
	        int value = arr[i];
	        int position=i;
	        while (position>0 && arr[position-1]>value){
	            arr[position] = arr[position-1];
	            position--;
	        }
	        arr[position] = value;
	    }//loop i
	}
	public static void main(String[] args){
        int[] arr = {10,30,20,60,40,50};
        Demo.insertionSort(arr);
        for(int i:arr){
            System.out.print(i+",");
        }
    }
}

3.3 时空复杂度

直接插入排序关键字比较次数和数据元素移动次数与数据元素的初始状态有关。在最好的情况下，待排序的序列是已经排好序的，每一趟插入，只需要比较一次就可以确定待插入的数据元素的位置，需要移动两次数据元素。因此总的关键字比较次数为$n-1$,总的数据元素移动次数为$2(n-1)$

在最坏的情况下，待排序的序列是反序的，每一趟中，待插入的数据元素需要与前面已排序序列的每一个数据元素进行比较，移动次数等于比较次数。因此，总的比较次数和移动次数都是$n(n-1)/2$

直接插入排序的时间复杂度为$O(n^2)$。直接插入排序需要一个单元的辅助存储单元，空间复杂度为$O(1)$。直接插入排序只在相邻的数据元素之间进行交换，它是一种稳定的排序方法。

最好情况$O(n)$；最坏情况$O(n^2)$；平均时间复杂度为：$O(n^2)$
空间复杂度：$O(1)$
稳定性：稳定

四、希尔排序（Shell Sort）

4.1 思想

希尔排序，也称递减增量排序算法，实质是分组插入排序。由 Donald Shell 于1959年提出。希尔排序是非稳定排序算法。

希尔排序的基本思想是：将数组列在一个表中并对列分别进行插入排序，重复这过程，不过每次用更长的列（步长更长了，列数更少了）来进行。最后整个表就只有一列了。将数组转换至表是为了更好地理解这算法，算法本身还是使用数组进行排序。

例如，假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]，如果我们以步长为5开始进行排序，我们可以通过将这列表放在有5列的表中来更好地描述算法，这样他们就应该看起来是这样：

1
2
3
4
13 14 94 33 82
25 59 94 65 23
45 27 73 25 39
10

然后我们对每列进行排序：

1
2
3
4
10 14 73 25 23
13 27 94 33 39
25 59 94 65 82
45

将上述四行数字，依序接在一起时我们得到：[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]。这时10已经移至正确位置了，然后再以3为步长进行排序：

1
2
3
4
5
6
10 14 73
25 23 13
27 94 33
39 25 59
94 65 82
45

排序之后变为：

1
2
3
4
5
6
10 14 13
25 23 33
27 25 59
39 65 73
45 94 82
94

最后以1步长进行排序（此时就是简单的插入排序了）。

4.2 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Demo {  
    public static void main(String[] args) {  
        int[] data = new int[] {10,30,20,60,40,50};  
        shellSort(data);  
        for(int i:data) {
        System.out.println(i);  }
    }
    public static void shellSort(int[] arr){
        int temp;
        for (int delta = arr.length/2; delta>=1; delta/=2){                              //对每个增量进行一次排序
            for (int i=delta; i<arr.length; i++){             
                for (int j=i; j>=delta && arr[j]<arr[j-delta]; j-=delta){ //注意每个地方增量和差值都是delta
                    temp = arr[j-delta];
                    arr[j-delta] = arr[j];
                    arr[j] = temp;
                }
            }//loop i
        }//loop delta
    }
}

上面源码的步长的选择是从n/2开始，每次再减半，直至为0。步长的选择直接决定了希尔排序的复杂度。在维基百科上有对于步长串行的详细介绍。

五、归并排序（Merge Sort）

5.1 思想

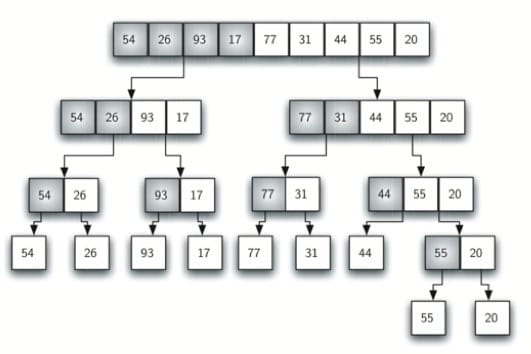
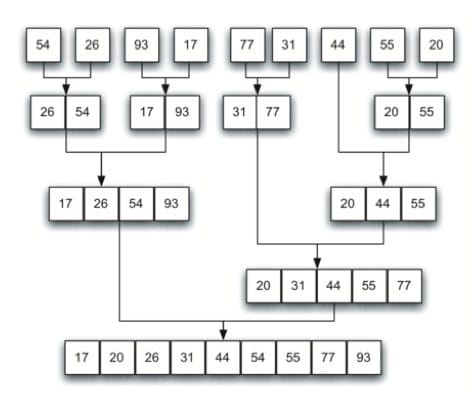
典型的是二路合并排序，将原始数据集分成两部分(不一定能够均分)，分别对它们进行排序，然后将排序后的子数据集进行合并，这是典型的分治法策略。

2019-05-17-164426.jpg

2019-05-17-164432.jpg

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public class Demo {  
    public static void main(String[] args) {  
        int[] data = new int[] {10,30,20,60,40,50};  
        mergesort(data); 
        for(int i:data) {
        		System.out.println(i); 
        	} 
    }
    public static void mergesort(int[] arr){
        sort(arr, 0, arr.length-1);
    }
    private static void sort(int[] a, int left, int right){
        //当left==right的时，已经不需要再划分了
        if (left<right){
            int middle = (left+right)/2;
            sort(a, left, middle);          //左子数组
            sort(a, middle+1, right);       //右子数组
            merge(a, left, middle, right);    //合并两个子数组
        }
    }
    // 合并两个有序子序列 arr[left, ..., middle] 和 arr[middle+1, ..., right]。temp是辅助数组。
    private static void merge(int arr[], int left, int middle, int right){
        int[] temp = new int[right - left + 1];
        int i=left;     
        int j=middle+1;
        int k=0;
        //将记录由小到大地放进temp数组
        while ( i<=middle && j<=right){
            if (arr[i] <=arr[j]){
                temp[k++] = arr[i++];
            }
            else{
                temp[k++] = arr[j++];
            }
        }
        while (i <=middle){
            temp[k++] = arr[i++];
        }
        while ( j<=right){
            temp[k++] = arr[j++];
        }
        //把数据复制回原数组
        for (i=0; i<k; ++i){
            arr[left+i] = temp[i];
        }
    }
   
}

5.3 时空复杂度

在归并排序中，进行一趟归并需要的关键字比较次数和数据元素移动次数最多为$n$，需要归并的趟数$log_{2}n$，故归并排序的时间复杂度为$O(nlog_{2}n)$。归并排序需要长度等于序列长度为$n$的辅助存储单元，故归并排序的空间复杂度为$O(n)$。归并排序是稳定的排序算法。

时间复杂度：$O(nlog_{2}n)$
空间复杂度：$O(n)$
稳定性：稳定

六、快速排序（Quick Sort）

6.1 思想

快速排序是图灵奖得主C.R.A Hoare于1960年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法（Divide-and-Conquer Method）

分治法的基本思想是：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题，然后将这些子问题组合为原问题的解。

利用分治法可将快速排序分为三步：

  1. 从数列中挑出一个元素作为“基准”（pivot）。
  2. 分区过程，将比基准数大的放到右边，小于或等于它的数都放到左边。这个操作称为“分区操作”，分区操作结束后，基准元素所处的位置就是最终排序后它的位置
  3. 再对“基准”左右两边的子集不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

6.2 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class Demo {  
    public static void main(String[] args) {  
        int[] data = new int[] {10,30,20,60,40,50};  
        quickSort(data);  
        for(int i:data) {
        System.out.println(i);  }
    }
    public static void quickSort(int[] arr){
        qsort(arr, 0, arr.length-1);
    }
    private static void qsort(int[] arr, int left, int right){
        if (left < right){
            int pivot=partition(arr, left, right);        //将数组分为两部分
            qsort(arr, left, pivot-1);                   //递归排序左子数组
            qsort(arr, pivot+1, right);                  //递归排序右子数组
        }
    }
    private static int partition(int[] arr, int left, int right){
        int pivot = arr[left];     //基准记录
        while (left<right){
            while (left<right && arr[right]>=pivot) --right;
            arr[left]=arr[right];             //交换比基准小的记录到左端
            while (left<right && arr[left]<=pivot) ++left;
            arr[right] = arr[left];           //交换比基准大的记录到右端
        }
        //扫描完成，基准到位
        arr[left] = pivot;
        //返回的是基准的位置
        return left;
    }
}

6.3 时空复杂度

时间复杂度：最好$O(nlog_2n)$；平均$O(nlog_2n)$，最坏：$O(n^2)$
空间复杂度：$O(log_2n)$
稳定性：不稳定

七、堆排序（Heap Sort）

7.1 思想

先上一张堆排序动画演示图：

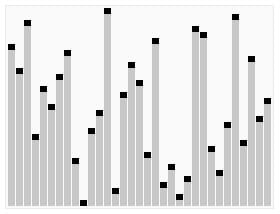
2019-05-17-164533.jpg

堆排序在 top K 问题中使用比较频繁。堆排序是采用二叉堆的数据结构来实现的，虽然实质上还是一维数组。堆（二叉堆）可以视为一棵完全的二叉树，完全二叉树的一个“优秀”的性质是，除了最底层之外，每一层都是满的，这使得堆可以利用数组来表示（普通的一般的二叉树通常用链表作为基本容器表示），每一个结点对应数组中的一个元素。

如下图，是一个堆和数组的相互关系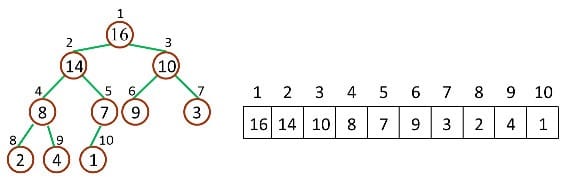
2019-05-17-164543.jpg

对于给定的某个结点的下标 i，可以很容易的计算出这个结点的父结点、孩子结点的下标：

  • Parent(i) = floor(i/2)，i 的父节点下标
  • Left(i) = 2i，i 的左子节点下标
  • Right(i) = 2i + 1，i 的右子节点下标

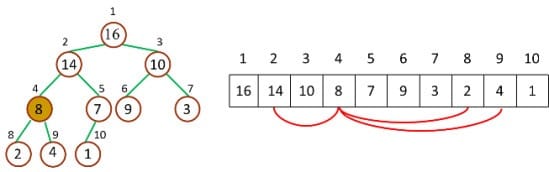
二叉堆具有以下性质：

  1. 父节点的键值总是大于或等于（小于或等于）任何一个子节点的键值。
  2. 每个节点的左右子树都是一个二叉堆（都是最大堆或最小堆）。

二叉堆一般分为两种：最大堆和最小堆。

最大堆的定义如下：

  • 最大堆中的最大元素值出现在根结点（堆顶）
  • 堆中每个父节点的元素值都大于等于其孩子结点（如果存在）

最小堆的定义如下：

  • 最小堆中的最小元素值出现在根结点（堆顶）
  • 堆中每个父节点的元素值都小于等于其孩子结点（如果存在）

【提问】
堆是怎么调整的，介绍大顶堆和小顶堆；

堆排序的原理如下：

步骤：

  1. 构造最大堆（Build_Max_Heap）：若数组下标范围为0~n，考虑到单独一个元素是大根堆，则从下标n/2开始的元素均为大根堆。于是只要从n/2-1开始，向前依次构造大根堆，这样就能保证，构造到某个节点时，它的左右子树都已经是大根堆。
  2. 堆排序（HeapSort）：由于堆是用数组模拟的。得到一个大根堆后，数组内部并不是有序的。因此需要将堆化数组有序化。思想是移除根节点，并做最大堆调整的递归运算。第一次将heap[0]与heap[n-1]交换，再对heap[0…n-2]做最大堆调整。第二次将heap[0]与heap[n-2]交换，再对heap[0…n-3]做最大堆调整。重复该操作直至heap[0]和heap[1]交换。由于每次都是将最大的数并入到后面的有序区间，故操作完后整个数组就是有序的了。
  3. 最大堆调整（Max_Heapify）：该方法是提供给上述两个过程调用的。目的是将堆的末端子节点作调整，使得子节点永远小于父节点 。

7.2 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
public class Demo {  
  
    public static void main(String[] args) {  
        int[] arr = { 50, 10, 90, 30, 70, 40, 80, 60, 20 };  
  
        // 堆排序  
        heapSort(arr);  
        for (int i = 0; i < arr.length; i++) {  
            System.out.print(arr[i] + " ");  
        }  
    }  
  
    /** 
     * 堆排序 
     */  
    private static void heapSort(int[] arr) {   
        // 将待排序的序列构建成一个大顶堆  
        for (int i = arr.length / 2; i >= 0; i--){   
            heapAdjust(arr, i, arr.length);   
        }            
        // 逐步将每个最大值的根节点与末尾元素交换，并且再调整二叉树，使其成为大顶堆  
        for (int i = arr.length - 1; i > 0; i--) {   
            swap(arr, 0, i); // 将堆顶记录和当前未经排序子序列的最后一个记录交换  
            heapAdjust(arr, 0, i); // 交换之后，需要重新检查堆是否符合大顶堆，不符合则要调整  
        }  
    }  
  
    /** 
     * 构建堆的过程 
     * @param arr 需要排序的数组 
     * @param i 需要构建堆的根节点的序号 
     * @param n 数组的长度 
     */  
    private static void heapAdjust(int[] arr, int i, int n) {  
        int child;  
        int father;   
        for (father = arr[i]; leftChild(i) < n; i = child) {  
            child = leftChild(i);  
              
            // 如果左子树小于右子树，则需要比较右子树和父节点  
            if (child != n - 1 && arr[child] < arr[child + 1]) {  
                child++; // 序号增1，指向右子树  
            }  
              
            // 如果父节点小于孩子结点，则需要交换  
            if (father < arr[child]) {  
                arr[i] = arr[child];  
            } else {  
                break; // 大顶堆结构未被破坏，不需要调整  
            }  
        }  
        arr[i] = father;  
    }  
  
    // 获取到左孩子结点  
    private static int leftChild(int i) {  
        return 2 * i + 1;  
    }  
      
    // 交换元素位置  
    private static void swap(int[] arr, int index1, int index2) {  
        int tmp = arr[index1];  
        arr[index1] = arr[index2];  
        arr[index2] = tmp;  
    }  
}

7.3 时空复杂度

堆排序在建立堆和调整堆的过程中会产生比较大的开销，在元素少的时候并不适用。但是，在元素比较多的情况下，还是不错的一个选择。尤其是在解决诸如“前n大的数”一类问题时，几乎是首选算法。

八、桶排序

桶排序 (Bucket sort)或所谓的箱排序的原理是将数组分到有限数量的桶子里，然后对每个桶子再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排序），最后将各个桶中的数据有序的合并起来。

排序过程：

  1. 假设待排序的一组数统一的分布在一个范围中，并将这一范围划分成几个子范围，也就是桶
  2. 将待排序的一组数，分档规入这些子桶，并将桶中的数据进行排序
  3. 将各个桶中的数据有序的合并起来

设有数组 array = [29, 25, 3, 49, 9, 37, 21, 43]，那么数组中最大数为 49，先设置 5 个桶，那么每个桶可存放数的范围为：0~9、10~19、20~29、30~39、40~49，然后分别将这些数放人自己所属的桶，如下图：

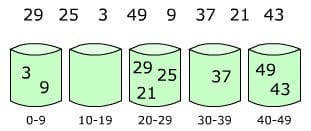
2019-05-17-164645.jpg
然后，分别对每个桶里面的数进行排序，或者在将数放入桶的同时用插入排序进行排序。最后，将各个桶中的数据有序的合并起来，如下图：

Data Structure Visualizations 提供了一个桶排序的分步动画演示。

九、各种排序方法的时空复杂度

9.1 时间复杂度

＂快些以$O(nlog_2n)$的速度归队＂

即快，希，归，堆都是$O(nlog_2n)$，其他都是$O(n^2)$，基数排序例外，是$O(d(n+rd))$

9.2 空间复杂度

  • 快排$O(log_2n)$
  • 归并$O(n)$
  • 基数$O(r_d)$
  • 其他$O(1)$

9.3 稳定性

＂心情不稳定，快些找一堆朋友聊天吧＂

即不稳定的有：快，希，堆

9.4 其他性质

  • 直接插入排序，初始基本有序情况下，是$O(n)$
  • 冒泡排序，初始基本有序情况下，是$O(n)$
  • 快排在初始状态越差的情况下算法效果越好．
  • 堆排序适合记录数量比较大的时候，从n个记录中选择k个记录．
  • 经过一趟排序，元素可以在它最终的位置的有：交换类的（冒泡，快排），选择类的（简单选择，堆）
  • 比较次数与初始序列无关的是：简单选择与折半插入
  • 排序趟数与原始序列有关的是：交换类的（冒泡和快排）

参考资料

维基百科：希尔排序，快速排序，归并排序，堆排序
排序算法可视化



应统联盟


连接十万名应统专业同学


阿药算法


打通算法面试任督二脉