数据结构与算法题解（1）：链表题解

链表相关题解java实现。

一、从尾到头打印链表（剑5）

输入一个链表的头结点，从尾到头反过来打印每个结点的值（注意不能改变链表的结构）。

解决这个问题肯定要遍历链表。遍历的顺序是从头到尾的顺序，可输出的顺序却是从尾到头。也就是说第一个遍历到的结点最后一个输出，而最后一个遍历到的结点第一个输出。这就是典型的“后进先出”，我们可以用栈实现这种顺序。没经过一个节点的时候，把该结点放到一个栈中。当遍历完整个链表后，再从栈顶开始逐个输出结点的值，此时输出的结点的顺序就翻转过来了。实现代码如下：

import java.util.Stack;
import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        Stack<Integer> stack = new Stack<>();
        while (listNode!=null){
            stack.push(listNode.val);
            listNode = listNode.next;
        }
        ArrayList<Integer> List = new ArrayList<>();
        while(!stack.isEmpty()){
            List.add(stack.pop());
        }
        return List;
    }
}

既然想到了用栈来实现这个函数，而递归在本质上就是一个栈结构，因此可用递归来实现。要实现反过来输出链表，我们每访问到一个节点的时候，先递归输出它后面的结点，再输出该结点自身，这样链表的输出结果就反过来了。实现代码如下：

import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        ArrayList<Integer> list=new ArrayList<Integer>();
        
        ListNode pNode=listNode;
        if(pNode!=null){
            if(pNode.next!=null){
                list=printListFromTailToHead(pNode.next);
            }
            list.add(pNode.val);
        }
        
        return list;
    }
}

二、在O(1)时间删除链表结点（剑13）

给定单向链表的头指针和一个结点指针，定义一个函数在O(1)时间删除该结点。

我们要删除结点i，先把i的下一个结点i.next的内容复制到i，然后在把i的指针指向i.next结点的下一个结点即i.next.next，它的效果刚好是把结点i给删除了。

此外还要考虑删除的结点是头尾结点、链表中只有一个结点、链表为空这几种情况。

java

public class DeleteNode {  
    /** 
     * 链表结点 
     */  
    public static class ListNode {  
        int value; // 保存链表的值  
        ListNode next; // 下一个结点  
    }  
    /** 
     * 给定单向链表的头指针和一个结点指针，定义一个函数在0(1)时间删除该结点, 
     * 【注意1：这个方法和文本上的不一样，书上的没有返回值，这个因为JAVA引用传递的原因， 
     * 如果删除的结点是头结点，如果不采用返回值的方式，那么头结点永远删除不了】 
     * 【注意2：输入的待删除结点必须是待链表中的结点，否则会引起错误，这个条件由用户进行保证】 
     * 
     * @param head        链表表的头 
     * @param toBeDeleted 待删除的结点 
     * @return 删除后的头结点 
     */  
    public static ListNode deleteNode(ListNode head, ListNode toBeDeleted) {  
        // 如果输入参数有空值就返回表头结点  
        if (head == null || toBeDeleted == null) {  
            return head;  
        }  
        // 如果删除的是头结点，直接返回头结点的下一个结点  
        if (head == toBeDeleted) {  
            return head.next;  
        }  
          // 下面的情况链表至少有两个结点  
        // 在多个节点的情况下，如果删除的是最后一个元素  
        if (toBeDeleted.next == null) {  
            // 找待删除元素的前驱  
            ListNode tmp = head;  
            while (tmp.next != toBeDeleted) {  
                tmp = tmp.next;  
            }  
            // 删除待结点  
            tmp.next = null;  
        }  
        // 在多个节点的情况下，如果删除的是某个中间结点  
        else {  
            // 将下一个结点的值输入当前待删除的结点  
            toBeDeleted.value = toBeDeleted.next.value;  
            // 待删除的结点的下一个指向原先待删除引号的下下个结点，即将待删除的下一个结点删除  
            toBeDeleted.next = toBeDeleted.next.next;  
        }  
        // 返回删除节点后的链表头结点  
        return head;  
    }

三、链表中倒数第K个结点（剑15）

输入一个链表，输出该链表中倒数第k个结点。为了符合大多数人的习惯，本题从1 开始计数，即链表的尾结点是倒数第1个结点。例如一个链表有6个结点，从头结点开始它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个结点的值为4的结点。

很自然的想法是先走到链表尾端，再从尾端回溯k步。可是我们从链表结点的定义可以看出本题中的链表是单向链表，单向链表的结点只有从前向后的指针而没有从后往前的指针，这种思路行不通。

既然不能从尾结点开始遍历链表，我们还是把思路回到头结点上来。假设整个链表有n个结点，那么倒数第k个结点就是从头结点开始往后走n-k+1步就可以了。如何得到结点树n？只需要从头开始遍历链表，每经过一个结点，计数器加1就行了。

也就是说我们需要遍历链表两次，第一次统计出链表中的结点的个数，第二次就能找到倒数第k个结点。但是面试官期待的解法是只需要遍历链表一次。

为了实现只遍历链表一次就能找到倒数第k个结点，我们可以定义两个指针。第一个指针从链表的头指针开始遍历向前走k-1步，第二个指针保持不动；从第k步开始，第二个指针也开始从链表的头指针开始遍历。由于两个指针的距离保持在k-1，当第一个（走在前面的）指针到达链表的尾结点时，第二个指针（走在后边的）指针正好是倒数第k个结点。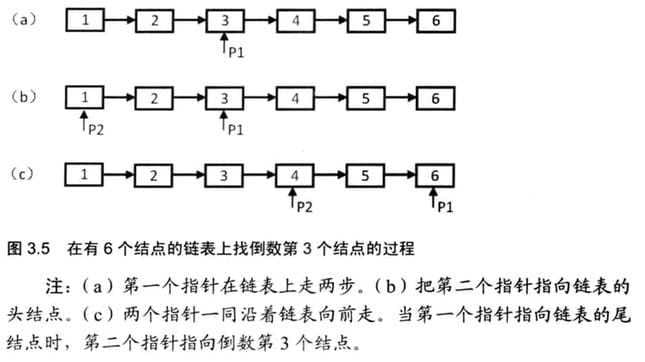

但是这样写出来的代码不够鲁棒，面试官可以找出三种办法让这段代码崩溃：

• 输入的ListHead为空指针。由于代码会试图访问空指针指向的内存，程序崩溃。
• 1. 输入的以ListHead为头结点的链表的结点总数少于k。由于在for循环中会在链表上向前走k-1步，仍然会由于空指针造成的程序奔溃。
• 1. 输入的参数k为0.由于k是一个无符号整数，那么在for循环中k-1得到的将不是-1，而是4294967295（无符号的0xFFFFFFFFF），因此for循环执行的次数远远超过我们的预计，同样也会造成程序崩溃。

面试过程中写代码特别要注意鲁棒性，若写出的代码存在多处崩溃的风险，那我们很可能和offer失之交臂。针对前面三个问题，分别处理。若输入的链表头指针为null，那么整个链表为空，此时查找倒数第k个结点自然应该返回null。若输入的k为0，也就是试图查找倒数第0个结点，由于我们计数是从1开始的，因此输入0是没有实际意义，也可以返回null。若链表的结点数少于k，在for循环中遍历链表可能会出现指向null的next，因此我们在for循环中应该加一个if循环。

代码如下：

java版本

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode FindKthToTail(ListNode head,int k) {
        if(head==null||k <=0){return null;}
        ListNode pAhead = head;
        ListNode pBehind = head;
        
        for(int i=1;i<k;i++){
            if(pAhead.next != null)
           	    {pAhead = pAhead.next;}
            else
                {return null;}
        }
        
        
        while(pAhead.next!=null)
            {
            pAhead = pAhead.next;
            pBehind = pBehind.next;        
        }
        return pBehind;
    }
}

python版本

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def FindKthToTail(self, head, k):
        # write code here
        if not head or k == 0:
            return None
        pAhead = head
        pBehind = None
        for i in xrange(0,k-1):
            if pAhead.next != None:                
          	    pAhead = pAhead.next
            else:
                return None
        pBehind = head
        while pAhead.next != None:
            pAhead = pAhead.next
            pBehind = pBehind.next
        return pBehind

四、反转链表（剑16）

定义一个函数，输入一个链表的头结点，反转该链表并输出反转后的头结点。链表结点定义如下：

public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}

解决与链表相关的问题总是有大量的指针操作，而指针操作的代码总是容易出错的。

为了正确地反转一个链表，需要调整链表中指针的方向。为了将调整指针这个复杂的过程分析清楚，可以借助图形来直观分析。在下图所示的链表中，h、i、j是3个相邻的结点。假设经过若干操作，我们已经把结点h之前的指针调整完毕，这些结点的next指向h，此时链表的结果如下所示：

其中（a）为一个链表，（b）把i之前的所有结点的next都指向前一个结点，导致链表在结点i、j之间断裂。

不难注意到，由于结点i的next指向了它的前一个结点，导致我们无法再链表中遍历到结点j。为了避免链表在结点i处断开，我们需要在调整结点i的next之前把结点j保存下来。

也就是说我们在调整结点i的next指针时，除了需要知道结点i本身之外，还需要前一个结点h，因为我们需要把结点i的next指向结点h。同时，我们还事先需要保存i的一个结点j，以防止链表断开。因此相应地我们需要定义3个指针，分别指向当前遍历到的结点、它的前一个结点及后一个结点。

最后我们试着找到反转后链表的头结点。不难分析出反转后链表的头结点是原始链表的尾结点。什么结点是尾结点？自然是next为null的结点。

$$pre\rightarrow head \rightarrow next$$

先保存next，即$next = head.next$再反转head的指针$head.next=pre $，链表结构变成

$$pre\leftarrow head \ \ \ next$$

接着向后移动结点$pre=head,head=next$

实现代码如下：

java版本

public class Solution {
    public ListNode ReverseList(ListNode head) {
       
        if(head==null)
            return null;
        //head为当前节点，如果当前节点为空的话，那就什么也不做，直接返回null；
        ListNode pre = null;
        ListNode next = null;
        //当前节点是head，pre为当前节点的前一节点，next为当前节点的下一节点
        //需要pre和next的目的是让当前节点从pre->head->next1->next2变成pre<-head next1->next2
        //即pre让节点可以反转所指方向，但反转之后如果不用next节点保存next1节点的话，此单链表就此断开了
        //所以需要用到pre和next两个节点
        //1->2->3->4->5
        //1<-2<-3 4->5
        while(head!=null){
            //做循环，如果当前节点不为空的话，始终执行此循环，此循环的目的就是让当前节点从指向next到指向pre
            //如此就可以做到反转链表的效果
            //先用next保存head的下一个节点的信息，保证单链表不会因为失去head节点的原next节点而就此断裂
            next = head.next;
            //保存完next，就可以让head从指向next变成指向pre了，代码如下
            head.next = pre;
            //head指向pre后，就继续依次反转下一个节点
            //让pre，head，next依次向后移动一个节点，继续下一次的指针反转
            pre = head;
            head = next;
        }
        //如果head为null的时候，pre就为最后一个节点了，但是链表已经反转完毕，pre就是反转后链表的第一个节点
        //直接输出pre就是我们想要得到的反转后的链表
        return pre;
    }
}

python版本

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    # 返回ListNode
    def ReverseList(self, pHead):
        # write code here
        if not pHead or not pHead.next:
            return pHead          
        pre = None        
        while pHead:
            next1 = pHead.next
            pHead.next = pre
            pre = pHead
            pHead = next1
        return pre

五、合并两个排序的链表（剑17）

输入两个递增排序的链表，合并这两个链表并使新链表中的结点仍然是按照递增排序的。例如下图中的链表1和链表2，则合并之后的升序链表3如下所示：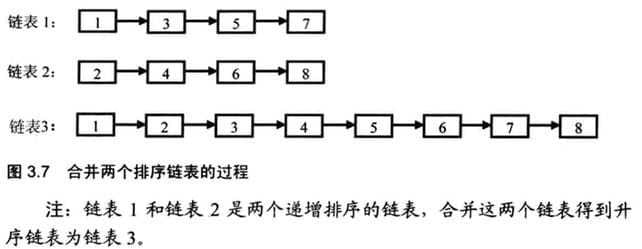

这是一个经常被各公司采用的面试题。在面试过程中，最容易犯两种错误：一是在写代码之前没有对合并的过程想清楚，最终合并出来的链表要么中间断开了，要么并没有做到递增排序；二是代码在鲁棒性方面存在问题，程序一旦有特殊的输入（如空链表）就会奔溃。
首先分析合并两个链表的过程。从合并两个链表的头结点开始。链表1的头结点的值小于链表2的头结点的值，因此链表1的头结点将是合并后链表的头结点。

继续合并剩余的结点。在两个链表中剩下的结点依然是排序的，因此合并这两个链表的步骤和前面的步骤是一样的。依旧比较两个头结点的值。此时链表2的头结点值小于链表1的头结点的值，因此链表2的头结点的值将是合并剩余结点得到的链表的头结点。把这个结点和前面合并链表时得到的链表的尾结点链接起来。

当我们得到两个链表中值较小的头结点并把它链接到已经合并的链表之后，两个链表剩余的结点依然是排序的，因此合并的步骤和之前的步骤是一样的。这是典型的递归过程，我们可以定义递归函数完成这一合并过程。（解决这个问题需要大量的指针操作，如没有透彻地分析问题形成清晰的思路，很难写出正确的代码）

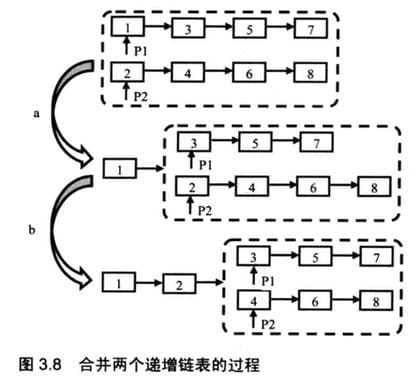
接下来解决鲁棒性问题，每当代码试图访问空指针指向的内存时程序就会奔溃，从而导致鲁棒性问题。本题中一旦输入空的链表就会引入空的指针，因此我们要对空链表单独处理。当第一个链表是空链表
，也就是它的头结点是一个空指针时，和第二个链表合并的结果就是第二个链表。同样，当输入的第二个链表的头结点是空指针的时候，和第一个链表合并得到的结果就是第一个链表。如果两个链表都为空，合并得到的是一个空链表。（由于有大量的指针操作，如果稍有不慎就会在代码中遗留很多与鲁棒性相关的隐患。建议应聘者在写代码之前全面分析哪些情况会引入空指针，并考虑清楚怎么处理这些空指针。）

代码如下：

java

public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {
        //新建一个头节点，用来存合并的链表。
        ListNode head=new ListNode(-1);
        head.next=null; 
        ListNode root=head;
        while(list1!=null&&list2!=null){
            if(list1.val<list2.val){
                head.next=list1;
                list1=list1.next;
            }else{
                head.next=list2;
                list2=list2.next;
            }
            head = head.next;
        }
        //把未结束的链表连接到合并后的链表尾部
        if(list1!=null){
            head.next=list1;
        }
        if(list2!=null){
            head.next=list2;
        }
        return root.next;
    }
}

java递归写法

public class Solution {
    public ListNode Merge(ListNode list1,ListNode list2) {
        if (list1==null) return list2;
        else if (list2==null) return list1;
        ListNode MergeHead = null;
        
        if (list.val<=list2.val){
            MergeHead = list1;
            MergeHead.next = Merge(list1.next,list2);
        }
        else 
        	{MergeHead = list2;
             MergeHead.next = Merge(list1,list2.next);
             }
        return MergeHead;
        
    }
}

六、复杂链表的复制（剑26）

输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点），返回结果为复制后复杂链表的head。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

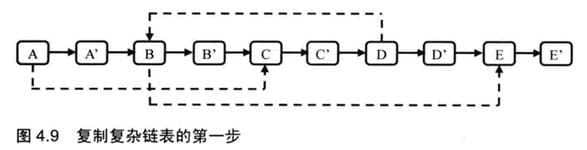
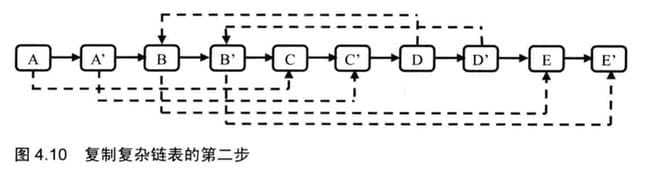
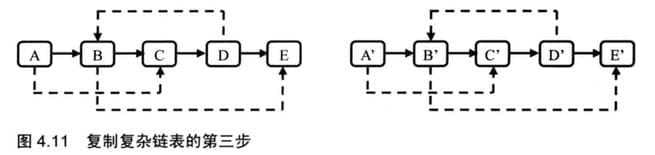
java

public class Solution {
    public RandomListNode Clone(RandomListNode pHead)
    {
        if (pHead == null) return null;
         //复制next 如原来是A->B->C 变成A->A'->B->B'->C->C'
        RandomListNode pCur = pHead;
        while (pCur != null)
        {
            RandomListNode node = new RandomListNode(pCur.label);
            node.next = pCur.next;
            pCur.next = node;
            pCur = node.next;
        }
         //复制random pCur是原来链表的结点 pCur.next是复制pCur的结点
        pCur = pHead;
        while (pCur!=null)
        {
            if (pCur.random!=null)
                pCur.next.random = pCur.random.next;
            pCur = pCur.next.next;
        }
         //拆分链表
        RandomListNode head = pHead.next;
        RandomListNode tmp = head;
        pCur = pHead;
        while(pCur.next!=null)
        {
            tmp = pCur.next;
            pCur.next = tmp.next;
            pCur = tmp;
        }
        return head;
    }
}

七、二叉搜索树与双向链表（剑27）

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

java

public class Solution {
    TreeNode head = null;
    TreeNode realHead = null;
    public TreeNode Convert(TreeNode pRootOfTree) {
        ConvertSub(pRootOfTree);
        return realHead//realHead是每个子树排序后的第一个结点，head是排序后的最后一个结点;
    }
     
    private void ConvertSub(TreeNode pRootOfTree) {
        //递归中序遍历
        if(pRootOfTree==null) return;
        ConvertSub(pRootOfTree.left);
        if (head == null) {
            //初始处
            head = pRootOfTree;
            realHead = pRootOfTree;
        } else {
            //前两句实现双向，第三句跳到下一个节点。
            head.right = pRootOfTree;
            pRootOfTree.left = head;
            head = pRootOfTree;
        }
        ConvertSub(pRootOfTree.right);
    }
}

八、两个链表的第一个公共结点（剑37）

输入两个链表找出他们的第一个公共结点。

面试的时候碰到这道题，很多应聘者的第一个想法就是蛮力法：在第一个链表上顺序遍历每个结点，每遍历到一个结点的时候，在第二个链表上顺序遍历每个结点。若第二个链表上有一个结点和第一个链表上的结点一样，说明两个链表在这个结点上重合，于是就找到了它们的公共结点。如果第一个链表的长度为m，第二个链表的长度为n，显然该方法的时间复杂度是O(mn)。

通常蛮力法不会是最好的办法，我们接下来试着分析有公共结点的两个链表有哪些特点。从链表结构的定义看出，这两个链表是单向链表。如果他们有公共的结点，那么这两个链表从某一结点开始，他们的next指向同一个结点。但由于是单向链表的结点，每个结点只有一个next，因此从第一个公共结点开始，之后的结点都是重合的，不可能再出现分叉。所以两个有公共结点而部分重合的链表，拓扑形状看起来像一个Y，而不是X。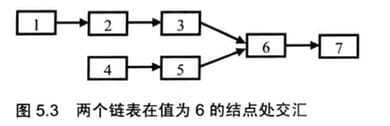

经过我们的分析发现，若两个链表有公共结点，那么公共结点出现在两个链表的尾部。如果我们从两个链表的尾部开始往前比较，最后一个相同的结点就是我们要找的结点。我们想到用栈的特点来解决这个问题：分别把两个链表的结点放入两个栈中，这样两个链表的尾结点就位于两个栈的栈顶，接下来比较两个栈顶的结点是否相同。若果相同，则把栈顶弹出接着比较下一个栈顶，直到找到最后一个相同的结点。

上面需要用到两个辅助栈。若链表的长度分别为m和n，那么空间复杂度是O(m+n)。这种思路的时间复杂度也是O(m+n)。和最开始的蛮力法相比，时间效率得到了提升，相当于是用空间换取时间效率。

之所以需要用到栈，是因为我们想同时遍历到达两个栈的尾结点。当两个链表的长度不相同时，如果我们从头开始遍历到达尾结点的时间就不一致。其实解决这个问题还有一个更简单的办法：首先遍历两个链表得到他们的长度，就能知道哪个链表比较长，以及长的链表比短的链表多几个结点。在第二次遍历的时候，在较长的链表上先走若干步，接着再同时在两个链表上遍历，找到的第一个相同的结点就是他们的第一个公共结点。

第三种思路和第二种思路相比，时间复杂度都是O(m+n)，但我们不再需要辅助的栈，因此提高了空间效率。实现代码如下：

java版本

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode FindFirstCommonNode(ListNode pHead1, ListNode pHead2) {
        ListNode current1 = pHead1;//链表1
        ListNode current2 = pHead2;//链表2
        if(pHead1 ==null||pHead2==null){return null;}//
        
        int len1 = getlistlength(pHead1);//链表1的长度
        int len2 = getlistlength(pHead2);//链表2的长度
        
        //若链表1长度大于链表2
        if(len1>=len2){
            int len=len1-len2;
            //遍历链表1，遍历长度为两链表长度差
            while (len>0){
                current1 = currentnext;
                len--;
                  
            }
        }
        //若链表2长度大于链表1
        else if(len1<len2){
            int len=len2-len1;
            //遍历链表2，遍历长度为两链表长度差
            while (len>0){
                current2=current2.next;
                len--;
            }
        }
        //开始齐头并进，直到找到第一个公共结点
        while(current1!=current2){
            current1 = currentnext;
            current2 = current2.next;
        }
        return current1;
    }
    //求指定链表的长度
    public static int getlistlength(ListNode pHead){
        int length = 0;
        ListNode current = pHead;
        while(current!=null){
            length++;
            current = current.next;
        }
        return length;
    }
}

python版本

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def FindFirstCommonNode(self, pHead1, pHead2):
        # write code here
        current1=pHead1
        current2=pHead2
        len1 = self.getlistlength(current1)
        len2 = self.getlistlength(current2)        
        if len1>=len2:            
            length = len1-len2
            while length>0:
                current1 = currentnext
                length=length-1                
        elif len1<len2:
            length = len2-len1
            while length>0:
                current2 = current2.next
                length=length-1               
        while current1!=current2:
            current1=currentnext
            current2=current2.next
        return current1
    
    def getlistlength(self,pHead):
        length =0
        current =pHead
        while current!=None:
            length=length+1
            current = current.next
        return length

九、圆圈中最后剩下的的数字（剑45）

0、…..，n-1这n个数字排成一个圆圈，从数字0开始每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。
约瑟夫环问题，用环形链表模拟圆圈的经典解法，

java

public class Solution{
    public int LastRemaining_Solution(int n, int m){
        if(m<=0||n<=0)return -1;
        //先构造循环链表
        ListNode head= new ListNode(0);//头结点, 值为0
        ListNode pre = head;
        ListNode temp = null;
        for(int i=1;i<n;i++){
            temp = new ListNode(i);
            pre.next = temp;
            pre = temp;
        }
        temp.next = head;//将第n-1个结点(也就是尾结点)指向头结点
        ListNode temp2 = null;
        
        while(n>=1){
            //每次都当前头结点找到第m个结点的前驱
            temp2=head;
            for(int i =1;i<m-1;i++){
                temp2 = temp2.next;
            }
            temp2.next = temp2.next.next;
            head = temp2.next;//设置当前头结点
            n--;
        }
        return head.val;
    }
}

java

public class Solution
{
    public int LastRemaining_Solution(int n, int m)
    {
        if(n==0||m==0)return -1;
        int last=0;
        for(int i=2;i<=n;i++)
        {
            last=(last+m)%i;
        }   
       return last ;
    }
}

十、链表中环的入口结点（剑56）

一个链表中包含环，如何找到环的入口结点？例如在下图的链表中，环的入口结点是结点3。

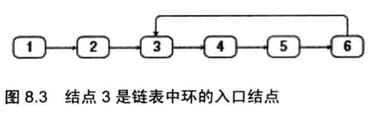
以3为例分析两个指针的移动规律。指针$P_1$和$P_2$在初始化时都指向链表的头结点。由于环中有4个结点，指针$P_1$先在链表上向前移动4步。接下来两个指针以相同的速度在链表上向前移动，直到它们相遇。它们相遇的结点正好是还的入口结点。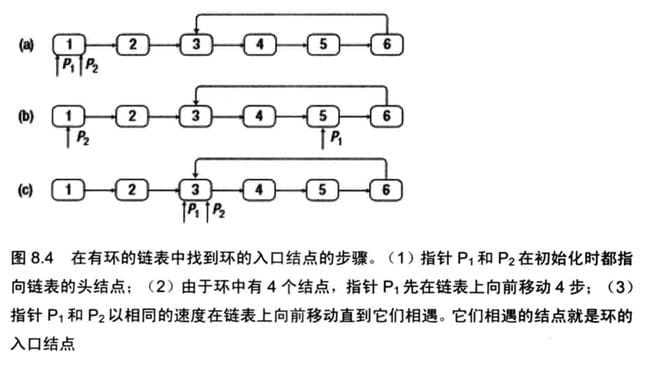

剩下的问题就是如何得到环中结点的数目。我们可以使用一快一慢两个指针。若两个指针相遇，说明链表中有环。两个指针相遇的结点一定是在环中的。可以从这个结点出发，一边继续向前移动一边计数，当再次回到这个结点时，就可以得到环中结点数了
实现代码如下：

java版本

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
	//找到一快一满指针相遇处的节点，相遇的节点一定是在环中
    public static ListNode meetingNode(ListNode pHead)
    {
        if(pHead == null){return null;}//空链表处理
        ListNode pslow = pHead.next;
        
        if(pslow == null){return null;}//无环链表处理
        
        ListNode pfast = pslow.next;
        while(pfast!=null && pslow!=null){
            if(pslow==pfast){return pfast;}
            
            pslow = pslow.next;//慢指针
            
            pfast = pfast.next;
            if(pfast!=null){
                pfast = pfast.next;
            }//块指针
            
        }
        return null;
    }
    
    public ListNode EntryNodeOfLoop(ListNode pHead){
        ListNode meetingNode=meetingNode(pHead);//相遇结点
        //环的结点个数
        if(meetingNode==null){return null;}//是否有环
        int nodesInLoop = 1;        
        ListNode p1=meetingNode;
        while(pnext!=meetingNode){
            p1=pnext;
            ++nodesInLoop;
        }
        //p1慢指针,先往前走
        p1=pHead;
        for(int i=0;i<nodesInLoop;i++){
            p1=pnext;
        }
        //p1,p2同步走，相遇的地方即为环入口
        ListNode p2=pHead;
        while(p1!=p2){
            p1=pnext;
            p2=p2.next;
        }
        return p1;
    } 
}

python 版本

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def meetingNode(self,pHead):
        if not pHead:
            return None
        pslow =pHead.next        
        if not pslow:
            return None
        pfast = pslow.next
        while pfast and pslow:
            if pslow==pfast:
                return pfast
            pslow = pslow.next
            
            pfast = pfast.next
            if pfast:
                pfast=pfast.next
        return None 
    def EntryNodeOfLoop(self, pHead):
        meetingNode = self.meetingNode(pHead)
        if not meetingNode:
            return None
        nodesInLoop = 1
        p1 = meetingNode
        while pnext!=meetingNode:
            p1=pnext
            nodesInLoop +=1
        p1 = pHead
        for i in xrange(0,nodesInLoop):
            p1=pnext
        p2=pHead
        while p1!=p2:
            p1=pnext
            p2=p2.next
        return p1

十一、删除链表中重复的结点（剑57）

在一个排序的链表中，如何删除重复的结点？如在下图中重复结点被删除之后，链表如下图所示：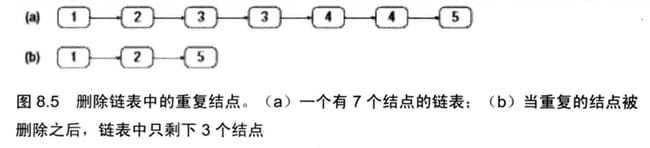

从头遍历整个链表。如果当前结点的值与下一个节点的值相同，那么它们就是重复的结点，都可以被删除。为了保证删除之后的链表仍然是相连的而没有中间断开，我们要把当前结点的前一个结点preNode和后面值比当前结点的值要大的结点相连。要确保preNode要始终与下一个没有重复的结点连接在一起。

实现代码如下：

java递归版

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    public ListNode deleteDuplication(ListNode pHead) {
        if (pHead == null || pHead.next == null) { // 只有0个或1个结点，则返回
            return pHead;
        }
        if (pHead.val == pHead.next.val) { // 当前结点是重复结点
            ListNode pNode = pHead.next;
            while (pNode != null && pNode.val == pHead.val) {
                // 跳过值与当前结点相同的全部结点,找到第一个与当前结点不同的结点
                pNode = pNode.next;
            }
            return deleteDuplication(pNode); // 从第一个与当前结点不同的结点开始递归
        } else { // 当前结点不是重复结点
            pHead.next = deleteDuplication(pHead.next); // 保留当前结点，从下一个结点开始递归
            return pHead;
        }
    }
}

python版本

# -*- coding:utf-8 -*-
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
class Solution:
    def deleteDuplication(self, pHead):
        if not pHead or not pHead.next:
            return pHead
        if pHead.val==pHead.next.val:
            pNode = pHead.next
            while pNode and pNode.val == pHead.val:
                 pNode = pNode.next
            return self.deleteDuplication(pNode)
        else:
            pHead.next = self.deleteDuplication(pHead.next)
            return pHead

java非递归

/*
 public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}
*/
public class Solution {
    public ListNode deleteDuplication(ListNode pHead)
    {
        if(pHead==null)return null;         
        ListNode preNode = null;
        ListNode node = pHead;
        while(node!=null){
            ListNode nextNode = node.next;
            boolean needDelete = false;
            //需要删除重复节点的情况
            if(nextNode!=null&&nextNode.val==node.val){
                needDelete = true;
            }
            //不重复结点不删除
            if(!needDelete){
                preNode = node;
                node = node.next;
            }
            //重复节点删除
            else{
                int value = node.val;
                ListNode toBeDel = node;
                //连续重复结点
                while(toBeDel != null && toBeDel.val == value){
                    nextNode = toBeDel.next;
                    toBeDel = nextNode;
                    if(preNode==null)
                        pHead = nextNode;
                    else
                        preNode.next = nextNode;
                    node = nextNode;
                }
            }
        }
         
        return pHead;
    }
}

十二、翻转部分链表(leetcode 92 Reverse Linked List II)

给了一个链表，第1个结点标号为1，把链表中标号在M到N区间的部分反转 （我写的很慢，面试官看不下去了，让我只说思路）

这道题是比较常见的链表反转操作，不过不是反转整个链表，而是从m到n的一部分。分为两个步骤，第一步是找到m结点所在位置，第二步就是进行反转直到n结点。反转的方法就是每读到一个结点，把它插入到m结点前面位置，然后m结点接到读到结点的下一个。总共只需要一次扫描，所以时间是O(n)，只需要几个辅助指针，空间是O(1)。代码如下：

java

public class Solution {
    public ListNode reverseBetween(ListNode head, int m, int n) {  
        if(head == null)  
            return null;  
        ListNode dummy = new ListNode(0);  
        dummy.next = head;  
        ListNode preNode = dummy;  
        int i=1;  
        while(preNode.next!=null && i<m)  
        {  
            preNode = preNode.next;  
            i++;  
        }  
        ListNode mNode = preNode.next;  
        ListNode cur = mNode.next;  
        while(cur!=null && i<n)  
        {  
            ListNode next = cur.next;  
            cur.next = preNode.next;  
            preNode.next = cur;  
            mNode.next = next;  
            cur = next;  
            i++;  
        }  
        return dummy.next;  
    } 
}

十三、链表插入排序(leetcode 147 Insertion Sort List)

这道题跟Sort List类似，要求在链表上实现一种排序算法，这道题是指定实现插入排序。插入排序是一种$O(n^2)$复杂度的算法，基本想法相信大家都比较了解，就是每次循环找到一个元素在当前排好的结果中相对应的位置，然后插进去，经过n次迭代之后就得到排好序的结果了。了解了思路之后就是链表的基本操作了，搜索并进行相应的插入。时间复杂度是排序算法的$O(n^2)$，空间复杂度是O(1)。代码如下：

java

public class Solution {
     public ListNode insertionSortList(ListNode head) {
		if( head == null ){
			return head;
		}
		
		ListNode helper = new ListNode(0); //new starter of the sorted list
		ListNode cur = head; //the node will be inserted
		ListNode pre = helper; //insert node between pre and pre.next
		ListNode next = null; //the next node will be inserted
		//not the end of input list
		while( cur != null ){
			next = cur.next;
			//find the right place to insert
			while( pre.next != null && pre.next.val < cur.val ){
				pre = pre.next;
			}
			//insert between pre and pre.next
			cur.next = pre.next;
			pre.next = cur;
			pre = helper;
			cur = next;
		}
		
		return helper.next;
	}
}

十四、链表归并排序(leetcode 148 Sort List)

链表排序，不允许直接交换节点的值，敲的有点bug，指针初始化有问题

这道题跟Insertion Sort List类似，要求我们用O(nlogn)算法对链表进行排序，但是并没有要求用哪一种排序算法，我们可以使用归并排序，快速排序，堆排序等满足要求的方法来实现。对于这道题比较容易想到的是归并排序，因为我们已经做过Merge Two Sorted Lists，这是归并排序的一个subroutine。剩下我们需要做的就是每次找到中点，然后对于左右进行递归，最后用Merge Two Sorted Lists把他们合并起来。代码如下：

java

public class Solution {
  
  public ListNode sortList(ListNode head) {
    if (head == null || head.next == null)
      return head;
        
    // step 1. cut the list to two halves
    ListNode prev = null, slow = head, fast = head;
    
    while (fast != null && fast.next != null) {
      prev = slow;
      slow = slow.next;
      fast = fast.next.next;
    }
    
    prev.next = null;
    
    // step 2. sort each half
    ListNode l1 = sortList(head);
    ListNode l2 = sortList(slow);
    
    // step 3. merge l1 and l2
    return merge(l1, l2);
  }
  
  ListNode merge(ListNode l1, ListNode l2) {
    ListNode l = new ListNode(0), p = l;
    
    while (l1 != null && l2 != null) {
      if (l1.val < l2.val) {
        p.next = l1;
        l1 = l1.next;
      } else {
        p.next = l2;
        l2 = l2.next;
      }
      p = p.next;
    }
    
    if (l1 != null)
      p.next = l1;
    
    if (l2 != null)
      p.next = l2;
    
    return l.next;
  }

}

十五、实现稀疏矩阵相乘

给定两个稀疏矩阵A和B，求AB。A的列数和B的行数相等。

面经：（链表，即每行的非零值存进单链表里。从面试官表情判断，应该说对了）

http://www.chongchonggou.com/g_5929864.html
例如：

A = [
  [ 1, 0, 0],
  [-1, 0, 3]
]

B = [
  [ 7, 0, 0 ],
  [ 0, 0, 0 ],
  [ 0, 0, 1 ]
]

     |  1 0 0 |   | 7 0 0 |   |  7 0 0 |
AB = | -1 0 3 | x | 0 0 0 | = | -7 0 3 |
                  | 0 0 1 |

这道题让我们实现稀疏矩阵相乘，稀疏矩阵的特点是矩阵中绝大多数的元素为0，而相乘的结果是还应该是稀疏矩阵，即还是大多数元素为0，那么我们使用传统的矩阵相乘的算法肯定会处理大量的0乘0的无用功，所以我们需要适当的优化算法，使其可以顺利通过OJ，我们知道一个$ i x k$ 的矩阵A乘以一个 $k x j$ 的矩阵B会得到一个$i x j$ 大小的矩阵C，那么我们来看结果矩阵中的某个元素$C[i][j]$是怎么来的。起始是$A[i][0]B[0][j] + A[i][1]B[1][j] + … + A[i][k]B[k][j]$，那么为了不重复计算0乘0，我们首先遍历A数组，要确保$A[i][k]$不为0，才继续计算，然后我们遍历B矩阵的第k行，如果$B[K][J]$不为0，我们累加结果矩阵$res[i][j] += A[i][k] B[k][j]$; 这样我们就能高效的算出稀疏矩阵的乘法，参见代码如下：

java

public int[][] multiply(int[][] A, int[][] B) {
    int rowA = A.length;
    int colA = A[0].length;
    int colB = B[0].length;
    int[][] res = new int[rowA][colB];

    for (int i = 0; i < rowA; i++) {
        for (int k = 0; k < colA; j++) {    
        	if (A[i][k] != 0) {// Check whether A[i][j]==0 to spare much time, because a sparse matrix has more than 95% zero elements 
	             for (int j = 0; j< colB; j++) { 
	                if (B[k][j] != 0) res[i][j] += A[i][k] * B[k][j]; 
	            }
        	}
        }
    }
    return res;   
}

再来看另一种方法，这种方法其实核心思想跟上面那种方法相同，稍有不同的是我们用一个链表来记录每一行中，各个位置中不为0的列数和其对应的值，这样就得到i个链表，然后我们遍历链表，取出每行中不为零的列数和值，然后遍历B中对应行进行累加相乘，参见代码如下：

java

public int[][] multiply(int[][] A, int[][] B) {
    int rowA = A.length;
    colA = A[0].length;
    colB = B[0].length;
    int[][] res = new int[rowA][colB];
    
    LinkedList<Point>[] rowsA = new LinkedList[rowA];
    for (int i = 0; i < rowA; i++) {// Create non-zero array for each row in A
    	rowsA[i] = new LinkedList();
        for (int j = 0; j < colA; j++) {   
        	if (A[i][j] != 0) {
        		rowsA[i].add(new Point(j, A[i][j]));
        	}
        }
    }
    
    for (int i = 0; i < rowA; i++) {// Only deal with non-zero elements in the above arrays 
        for (int j = 0; j < rowsA[i].size(); j++) {
        	int col = rowsA[i].get(j).x;
        	int val = rowsA[i].get(j).y;
	             for (int k = 0; k < colB; k++) { 
	                res[i][k] += val * B[col][k]; 
        	}
        }
    }
    return res;   
}

十六、排序链表中找出和为给定值的一段链表

排序链表中找出和为给定值的一段链表

面经中出现过的链表题：

• 二、如何在O(1)时间删除链表节点；
• 三、第一题是链表倒数第 k 节点；如何找链表倒数第K个结点（联系这个题目，两链表找交点的题就可以在O(1)空间解决了）；单链表如何判断有环；链表中倒数第K个结点
• 四、反转链表递归、非递归；链表反转；链表逆序。。正中我下怀~；写程序 翻转链表；给了个单链表逆置，写代码；用C/C++实现单链表的反转。
• 六、复杂链表的复制
• 七、二叉搜索树转换成一个排好序的双向链表；上网搜搜有怎样将二叉排序树变成双向链表
• 八、两个相交链表如何找交点（我说了用栈保存每个链表节点的方法，他问有没有O(1)空间解法，一时没想到）；判断两条链表是否交叉
• 十、确定链表中环的起始位置
• 十二、翻转部分链表(Reverse Linked List II)
• 十三、链表插入排序(Insertion Sort List)
• 十四、链表归并排序(Sort List)
• 十六、排序链表中找出和为给定值的一段链表