数据结构与算法题解（4）：二叉树题解

二叉树相关题解java实现。

一、重建二叉树（剑6）

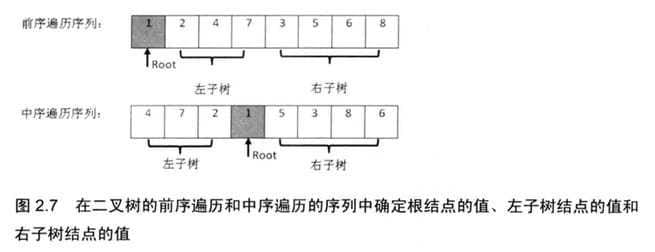
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

1. 根据前序遍历的特点，我们知道根结点为1
2. 观察中序遍历。其中root节点G左侧的472必然是root的左子树，G右侧的5386必然是root的右子树。
3. 观察左子树472，左子树的中的根节点必然是大树的root的leftchild。在前序遍历中，大树的root的leftchild位于root之后，所以左子树的根节点为2。
4. 同样的道理，root的右子树节点5386中的根节点也可以通过前序遍历求得。在前序遍历中，一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树，并且遍历的左子树的第一个节点就是左子树的根节点。同理，遍历的右子树的第一个节点就是右子树的根节点。
5. 观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了。

该步递归的过程可以简洁表达如下：

1. 确定根,确定左子树，确定右子树。
2. 在左子树中递归。
3. 在右子树中递归。
4. 打印当前根。

递归代码如下：

public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] in) { 
        return reConBTree(pre,0,pre.length-1,in,0,in.length-1);
    }
    public TreeNode reConBTree(int [] pre,int preleft,int preright,int [] in,int inleft,int inright){
        if(preleft > preright || inleft> inright)//当到达边界条件时候返回null
            return null;
        //新建一个TreeNode
        TreeNode root = new TreeNode(pre[preleft]);
        //对中序数组进行输入边界的遍历
        for(int i = inleft; i<= inright; i++){
            if(pre[preleft] == in[i]){
                //重构左子树，注意边界条件
                root.left = reConBTree(pre,preleft+1,preleft+i-inleft,in,inleft,i-1);
                //重构右子树，注意边界条件
                root.right = reConBTree(pre,preleft+i+1-inleft,preright,in,i+1,inright);
            }
        }
        return root;      
    }
}
``` 


## 二、树的子结构（剑18）
输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

要查找树A中是否存在和树B结构一样的子树，我们可以分成两步：第一步在树A中找到和B的根结点的值一样的结点R，第二步再判断树A以R为根结点的子树是不是包含和树B一样的结构。

第一步在树A中查找与根结点的值一样的结点，实际上就是树的遍历。对二叉树这种数据结构熟悉的读者自然知道可以用递归的方法去遍历，也可以用循环的方法去遍历。由于递归的代码实现比较简洁，面试时如果没有特别要求，通常会采用递归的方式。参考代码如下：
>java第一步

```java
public boolean HasSubtree(TreeNode root1,TreeNode root2) {
        boolean result = false;
        //一定要注意边界条件的检查，即检查空指针。否则程序容易奔溃，面试时尤其要注意。这里当Tree1和Tree2都不为零的时候，才进行比较。否则直接返回false
        if(root1!=null&&root2!=null){
        ////如果找到了对应Tree2的根节点的点
            if(root1.val==root2.val){
            //以这个根节点为为起点判断是否包含Tree2
                result = DoesTree1HaveTree2(root1,root2);
            }
            //如果找不到，那么就再去root的左儿子当作起点，去判断是否包含Tree2
            if(!result){
                result=HasSubtree(root1.left,root2);
            }
            //如果还找不到，那么就再去root的右儿子当作起点，去判断是否包含Tree2
            if(!result){
                result=HasSubtree(root1.right,root2);
            }
        }
        return result;
        
    }

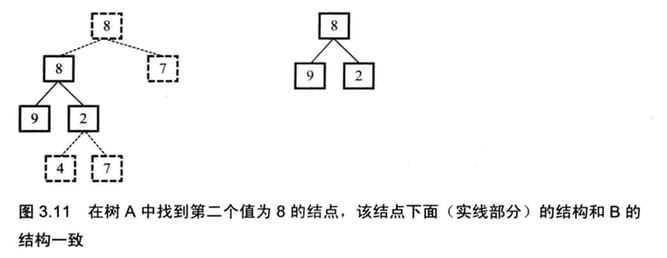
第二步是判断树A中以R为根结点的子树是不是和树B具有相同的结构。同样，我们也可以用递归的思路来考虑：如果结点R的值和树B的根结点不同，则以R为根结点的子树和树B一定不具有相同的结点；如果他们的值相同，则递归地判断它们各自的左右结点的值是不是相同。递归的终止条件是我们达到了树A或者树B的叶结点。

代码如下：

java

public boolean DoesTree1HaveTree2(TreeNode root1,TreeNode root2){
       //如果Tree2已经遍历完了都能对应的上，返回true
        if(root2==null){
            return true;
        }
        //如果Tree2还没有遍历完，Tree1却遍历完了。返回false
        if(root1==null){
            return false;
        }
         //如果其中有一个点没有对应上，返回false
        if(root1.val!=root2.val){
            return false;
        }
        //如果根节点对应的上，那么就分别去左右子节点里面匹配
        return DoesTree1HaveTree2(root1.left,root2.left)&&DoesTree1HaveTree2(root1.right,root2.right);
    }

二叉树相关的代码有大量的指针操作，每一次使用指针的时候，我们都要问自己这个指针有没有可能是NULL，如果是NULL该怎么处理。

三、二叉树的镜像（剑19）

操作给定的二叉树，将其变换为源二叉树的镜像。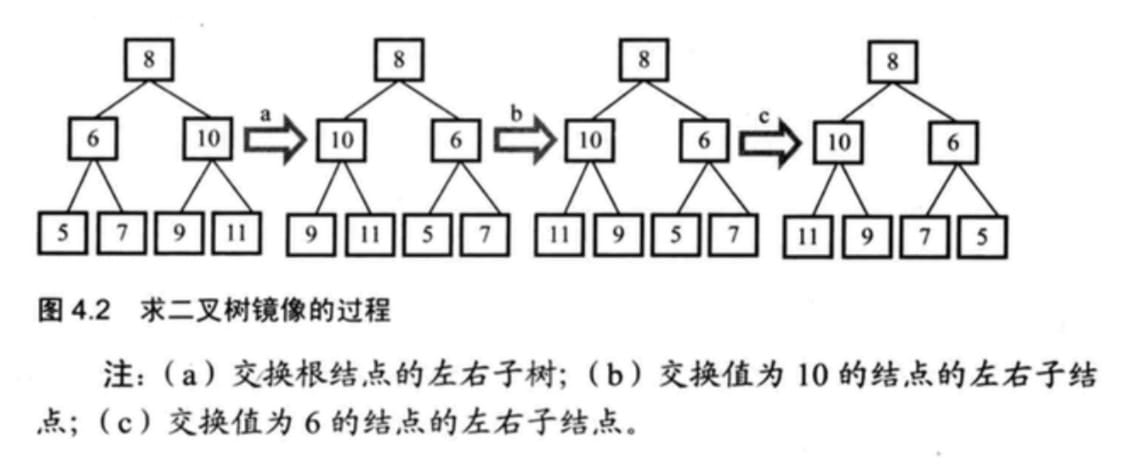

public class Solution {
    public void Mirror(TreeNode root) {
        //边界
        if(root==null)
            return;
        if(root.left==null&&root.right==null)
            return;
        //交换左右子树
        TreeNode temp = root.left;
        root.left=root.right;
        root.right=temp;
        //递归
        if(root.left!=null){
            Mirror(root.left);
        }
        if(root.right!=null){
            Mirror(root.right);
        }
        
    }
}

四、从上往下打印二叉树（剑23）

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

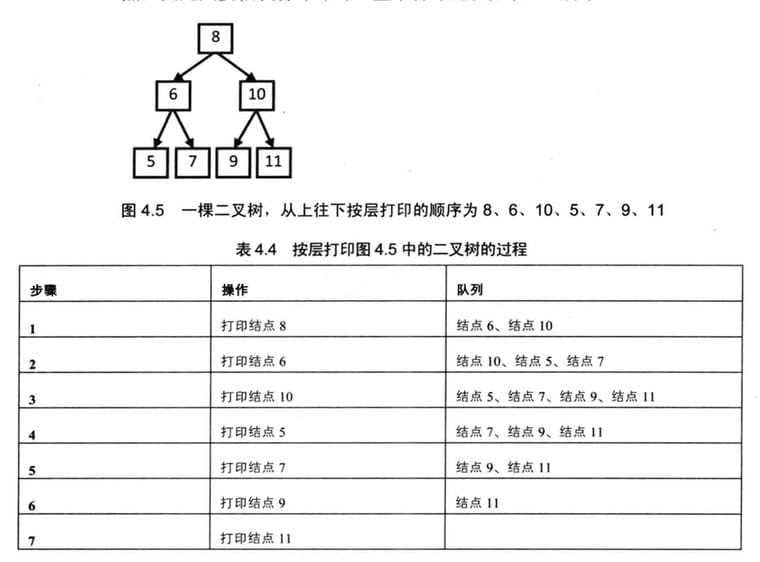
每次打印一个结点时，如果该结点有子结点，则把该结点的子结点放到队列的末尾。接下来到队列的头部取出最早进入队列的结点，重复前面的打印操作。

java

import java.util.ArrayList;
import java.util.LinkedList;
public class Solution {
    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        ArrayList<Integer> List=new ArrayList<Integer>();
        if(root==null){return List;}
        
        LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
        queue.add(root);//先把根结点加入队列q
        
        while(!queue.isEmpty()){//队列非空时
            TreeNode treenode=queue.remove();//取出队列头结点
            if(treenode.left!=null){queue.add(treenode.left);}//向队列加入左孩子（若有）
            if(treenode.right!=null){queue.add(treenode.right);}//向队列加入右孩子（若有）
            List.add(treenode.val);//加到打印列表中
        }
        return List;        
    }
}

五、二叉搜索树的后序遍历序列（剑24）

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

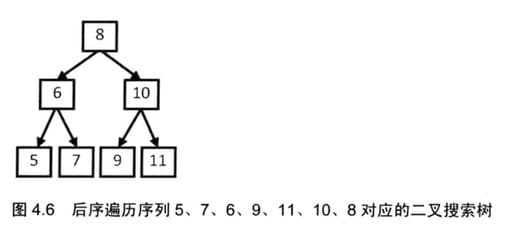
在后序遍历得到的序列中，最后一个数字是树的根结点的值。数组中前面的数字可以分成两部分：第一部分是左子树结点的值，它们都比根结点小；第二部分是右子树结点的值，它们都比根结点大。

java

import java.util.Arrays;
public class Solution {
    public boolean VerifySquenceOfBST(int [] sequence) {
        int length = sequence.length;
        if(sequence==null||length==0){return false;}
        int root = sequence[length-1];//根结点
        int i=0; //外部初始化     
        //找到左子树的最后一个结点位置
        for(;i<length-1;i++){
            if(sequence[i]>root){
                break;
            }
        }    
        //如果右子树的结点值小于根结点的值，则返回false
        for(int j=i;j<length-1;j++){
            if(sequence[j]<root){
                return false;
            }
        }    
        //初始化
        boolean left=true;
        boolean right=true;
        //递归左右子树
        if(i>0){
            left = VerifySquenceOfBST(Arrays.copyOfRange(sequence,0,i));//Arrays的copyOfRange方法
        }
        if(i<length-1){
            right = VerifySquenceOfBST(Arrays.copyOfRange(sequence,i,length-1));
        }
        return left&&right;                
    }
}

六、二叉树中和为某一值的路径（剑25）

输入一颗二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。

java

public class Solution {
    private ArrayList<ArrayList<Integer>> listAll = new ArrayList<ArrayList<Integer>>();
    private ArrayList<Integer> list = new ArrayList<Integer>();
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
        if(root == null) return listAll;
        list.add(root.val);
        target -= root.val;//每次减去结点的值
        //如果target等于0，则说明这条路径和为target，添加到listAll中
        if(target == 0 && root.left == null && root.right == null)
            listAll.add(new ArrayList<Integer>(list));//因为add添加的是引用，如果不new一个的话，后面的操作会更改listAll中list的值
        //向左孩子递归
        if(root.left!=null)FindPath(root.left, target);
        //向右孩子递归
        if(root.right!=null)FindPath(root.right, target);
        //如果不满足条件，则回到父节点；
        list.remove(list.size()-1);
        return listAll;
    }
}

七、二叉搜索树与双向链表（剑27）

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向。

java

public class Solution {
    TreeNode head = null;
    TreeNode realHead = null;
    public TreeNode Convert(TreeNode pRootOfTree) {
        ConvertSub(pRootOfTree);
        return realHead//realHead是每个子树排序后的第一个结点，head是排序后的最后一个结点;
    }
     
    private void ConvertSub(TreeNode pRootOfTree) {
        //递归中序遍历
        if(pRootOfTree==null) return;
        ConvertSub(pRootOfTree.left);
        if (head == null) {
            //初始处
            head = pRootOfTree;
            realHead = pRootOfTree;
        } else {
            //前两句实现双向，第三句跳到下一个节点。
            head.right = pRootOfTree;
            pRootOfTree.left = head;
            head = pRootOfTree;
        }
        ConvertSub(pRootOfTree.right);
    }
}

八、二叉树的深度（剑39.1）

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

Java 经典的求二叉树深度 递归写法

java

public class Solution {
    public int TreeDepth(TreeNode root) {
        if(root==null)return 0;
        int nleft = TreeDepth(root.left);
        int nright = TreeDepth(root.right);
        return nleft>nright?(nleft+1):(nright+1);
    }
}

九、平衡二叉树（剑39.2）

输入一棵二叉树，判断该二叉树是否是平衡二叉树。

有了求二叉树的深度的经验之后，我们就很容易想到一个思路：在遍历树的每个结点的时候，调用函数TreeDepth得到它的左右子树的深度。如果每个结点的左右子树的深度相差都不超过1，按照定义它就是一颗平衡的二叉树。

java

public class Solution {
    public boolean IsBalanced_Solution(TreeNode root) {
        if(root==null)return true;
        int left = TreeDepth(root.left);
        int right = TreeDepth(root.right);
        int diff = left-right;
        if(diff>1||diff<-1)
            return false;
        return IsBalanced_Solution(root.left)&&IsBalanced_Solution(root.right);
        
    }
    public int TreeDepth(TreeNode root) {
        if(root==null)return 0;
        int nleft = TreeDepth(root.left);
        int nright = TreeDepth(root.right);
        return nleft>nright?(nleft+1):(nright+1);
    }
}

十、二叉搜索树的最低公共祖先（剑50.1）

二叉搜索树是经过排序的，位于左子树的节点都比父节点小，位于右子树的节点都比父节点大。既然要找最低的公共祖先节点，我们可以从根节点开始进行比较。若当前节点的值比两个节点的值都大，那么最低的祖先节点一定在当前节点的左子树中，则遍历当前节点的左子节点；反之，若当前节点的值比两个节点的值都小，那么最低的祖先节点一定在当前节点的右子树中，则遍历当前节点的右子节点；这样，直到找到一个节点，位于两个节点值的中间，则找到了最低的公共祖先节点。

java

public class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null||root==q||root==p)return root;
        if(root.val>p.val&&root.val>q.val){
            return lowestCommonAncestor(root.left,p,q);
        }else if(root.val<p.val&&root.val<q.val){
            return lowestCommonAncestor(root.right,p,q);
        }else return root;
        
    }
}

十一、普通二叉树的最低公共祖先（剑50.2）

一种简单的方法是DFS分别寻找到两个节点p和q的路径，然后对比路径，查看他们的第一个分岔口，则为LCA。
这个思路比较简单，代码写起来不如下面这种方法优雅：

我们仍然可以用递归来解决，递归寻找两个带查询LCA的节点p和q，当找到后，返回给它们的父亲。如果某个节点的左右子树分别包括这两个节点，那么这个节点必然是所求的解，返回该节点。否则，返回左或者右子树（哪个包含p或者q的就返回哪个）。复杂度O(n)

java

public class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root==null||root==p||root==q){return root;}
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if(left!=null&&right!=null)return root;
        return left!=null? left:right;
        
    }
}

十二、二叉树的下一个结点（剑58）

给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

我们可发现分成两大类：

1. 有右子树的，那么下个结点就是右子树最左边的点；（eg：D，B，E，A，F，C，G）
2. 没有右子树的，也可以分成两类，a)是父节点左孩子（eg：N，I，L） ，那么父节点就是下一个节点 ； b)是父节点的右孩子（eg：H，J，K，M）找他的父节点的父节点的父节点…直到当前结点是其父节点的左孩子位置。如果没有eg：M，那么他就是尾节点。

   java

public class Solution {
    public TreeLinkNode GetNext(TreeLinkNode pNode)
    {
        if(pNode==null){return null;}
        if(pNode.right!=null){
            pNode = pNode.right;
            while(pNode.left!=null){
                pNode = pNode.left;
            }
            return pNode;
        }
        while(pNode.next!=null){
            if(pNode.next.left==pNode)return pNode.next;
            pNode = pNode.next;
        }
        return null;             
    }
}

十三、对称的二叉树（剑59）

请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

如果先序遍历的顺序分为两种先左后右和先右后左两种顺序遍历，如果两者相等说明二叉树是对称的二叉树

java

public class Solution {
    boolean isSymmetrical(TreeNode pRoot){
        return isSymmetrical(pRoot,pRoot);        
    }
    boolean isSymmetrical(TreeNode pRoot1,TreeNode pRoot2){
        if(pRoot1==null&&pRoot2==null)return true;
        if(pRoot1==null||pRoot2==null)return false;
        if(pRoot1.val==pRoot2.val){return
            isSymmetrical(pRoot1.left,pRoot2.right)&&isSymmetrical(pRoot1.right,pRoot2.left);
        }else 
            return false;
    }
}

十四、把二叉树打印成多行（剑60）

从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。
用end记录每层结点数目，start记录每层已经打印的数目，当start=end，重新建立list，开始下一层打印。

java

public class Solution {
    ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> result = new ArrayList<ArrayList<Integer>>();
        if(pRoot==null){return result;}
        LinkedList<TreeNode> queue = new LinkedList<TreeNode>();
        ArrayList<Integer> list = new ArrayList<Integer>();
        queue.add(pRoot);
        int start = 0,end = 1;
        while(!queue.isEmpty()){
            TreeNode treenode = queue.remove();
            list.add(treenode.val);
            start++;
            if(treenode.left!=null){queue.add(treenode.left);}
            if(treenode.right!=null){queue.add(treenode.right);} 
            if(start==end){
                end = queue.size();
                start = 0;
                result.add(list);
                list = new ArrayList<Integer>();
            }
        }
        return result;
    }    
}

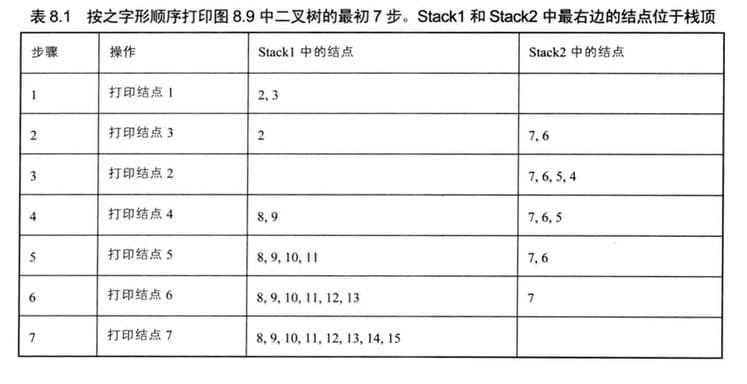
十五、按S型打印二叉树（剑61）

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

java

import java.util.ArrayList;
import java.util.Stack;

public class Solution {
    public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        ArrayList<ArrayList<Integer>> alist =new ArrayList<ArrayList<Integer>>();
        if(pRoot==null)return alist;
        Stack<TreeNode> stack1 = new Stack<TreeNode>();
        stack1.add(pRoot);
        Stack<TreeNode> stack2 = new Stack<TreeNode>();
        
        while(!stack1.isEmpty()||!stack2.isEmpty()){
            if(!stack1.isEmpty()){
                ArrayList<Integer> alist2 = new ArrayList<Integer>();           
                while(!stack1.isEmpty()){
                    TreeNode treenode=stack1.pop();
                    alist2.add(treenode.val);
                    if(treenode.left!=null){
                        stack2.add(treenode.left);
                    }
                    if(treenode.right!=null){
                        stack2.add(treenode.right);
                    }                
                }
                alist.add(alist2);
            }
            
            else{
                ArrayList<Integer> alist2 = new ArrayList<Integer>();
                while(!stack2.isEmpty()){
                    TreeNode treenode = stack2.pop();
                    alist2.add(treenode.val);
                    if(treenode.right!=null){
                        stack1.add(treenode.right);                        
                    }
                    if(treenode.left!=null){
                        stack1.add(treenode.left);
                    }
                }
                alist.add(alist2);
                
            }
        }
        return alist;

    }
}

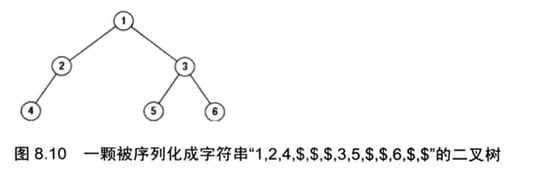
十六、序列化与反序列化二叉树（剑62）

请实现两个函数，分别用来序列化和反序列化二叉树
算法思想：根据前序遍历规则完成序列化与反序列化。所谓序列化指的是遍历二叉树为字符串；所谓反序列化指的是依据字符串重新构造成二叉树。

依据前序遍历序列来序列化二叉树，因为前序遍历序列是从根结点开始的。当在遍历二叉树时碰到Null指针时，这些Null指针被序列化为一个特殊的字符“#”。另外，结点之间的数值用逗号隔开。

java

public class Solution {
    int index = -1;   //计数变量
  
    String Serialize(TreeNode root) {
        StringBuilder sb = new StringBuilder();//新建字符串
        if(root == null){
            sb.append("#,");
            return sb.toString();
        }
        //递归
        sb.append(root.val + ",");
        sb.append(Serialize(root.left));
        sb.append(Serialize(root.right));
        return sb.toString();
  }
    TreeNode Deserialize(String str) {
        index++;
        //int len = str.length();
        //if(index >= len){
        //    return null;
       // }
        String[] strr = str.split(",");
        TreeNode node = null;
        if(!strr[index].equals("#")){
            node = new TreeNode(Integer.valueOf(strr[index]));
            node.left = Deserialize(str);
            node.right = Deserialize(str);
        }
        return node;
  }
}

十七、二叉搜索树的第K个结点（剑63）

给定一颗二叉搜索树，请找出其中的第k大的结点。例如在下图二叉搜索树里，按结点数值大小顺序第三个结点的值是4.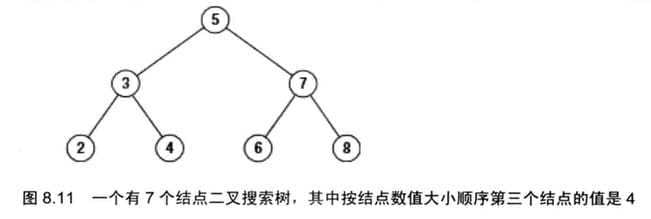

如果按照中序遍历的顺序遍历一颗二叉搜索树，遍历序列的数值是递增排序的，只需要用中序遍历算法遍历一颗二叉搜索树，就很容易找出它的第K大的结点。

java

public class Solution {
   int index = 0; //计数器
    TreeNode KthNode(TreeNode root, int k)
    {
        if(root != null){ //中序遍历寻找第k个
            TreeNode node = KthNode(root.left,k);
            if(node != null)
                return node;
            index ++;
            if(index == k)
                return root;
            node = KthNode(root.right,k);
            if(node != null)
                return node;
        }
        return null;
    }
}

十八、数据流中的中位数（剑64）

Java的PriorityQueue是从JDK1.5开始提供的新的数据结构接口，默认内部是自然排序，结果为小顶堆，也可以自定义排序器，比如下面反转比较，完成大顶堆。

为了保证插入新数据和取中位数的时间效率都高效，这里使用大顶堆+小顶堆的容器，并且满足：

1. 两个堆中的数据数目差不能超过1，这样可以使中位数只会出现在两个堆的交接处；
2. 大顶堆的所有数据都小于小顶堆，这样就满足了排序要求。

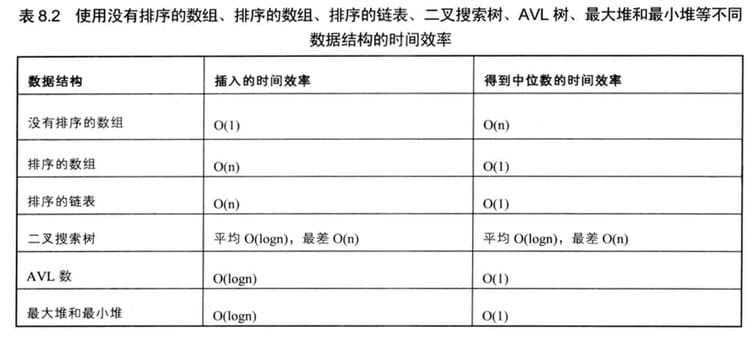
java

import java.util.Comparator;
import java.util.PriorityQueue;
 
public class Solution {
    int count=0;
    PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
    PriorityQueue<Integer> maxHeap = new PriorityQueue<Integer>(11, new Comparator<Integer>() {
        @Override
        public int compare(Integer o1, Integer o2) {
            //PriorityQueue默认是小顶堆，实现大顶堆，需要反转默认排序器
            return o2.compareTo(o1); 
        }
    });
 
    public void Insert(Integer num) {
    if (count %2 == 0) {//当数据总数为偶数时，新加入的元素，应当进入小根堆
        //（注意不是直接进入小根堆，而是经大根堆筛选后取大根堆中最大元素进入小根堆）
        //1.新加入的元素先入到大根堆，由大根堆筛选出堆中最大的元素
        maxHeap.offer(num);
        int filteredMaxNum = maxHeap.poll();
        //2.筛选后的【大根堆中的最大元素】进入小根堆
        minHeap.offer(filteredMaxNum);
    } else {//当数据总数为奇数时，新加入的元素，应当进入大根堆
        //（注意不是直接进入大根堆，而是经小根堆筛选后取小根堆中最大元素进入大根堆）
        //1.新加入的元素先入到小根堆，由小根堆筛选出堆中最小的元素
        minHeap.offer(num);
        int filteredMinNum = minHeap.poll();
        //2.筛选后的【小根堆中的最小元素】进入大根堆
        maxHeap.offer(filteredMinNum);
    }
    count++;
}
    
public Double GetMedian() {
    if (count %2 == 0) {
        return new Double((minHeap.peek() + maxHeap.peek())) / 2;
    } else {
        return new Double(minHeap.peek());
    }
}
}

十九、 二叉树最大路径和（leetcode 124）

一个很有意思的问题，一个社区，所有的房子构成一棵二叉树，每个房子里有一定价值的财物，这棵二叉树有一个根节点root。如果相邻的两座房子同时被进入，就会触发警报。一个小偷，最初只能访问root节点，并可以通过二叉树的边访问房子（注：访问不意味着进入），请问不触发警报的前提下他能偷到的财物的最大价值是多少？

以下面这棵二叉树为例，最多能偷走3+3+1=7的财物    
     3 
    / \ 
   2   3 
    \     \ 
     3     1

分析：
这个问题乍一看上去可能没什么思路，但是如果是用递归，可以很优雅的解决这个问题，这需要读者对递归有比较深刻的理解。下面给出解决这个问题的java代码：

import java.util.HashMap;
import java.util.Map;
import common.TreeNode;

public class Solution {
	//使用一个cache 缓存以每个节点为根节点的rob方法返回值，减少计算量
    Map<TreeNode, Integer> cache = new HashMap<TreeNode, Integer>();
    public int rob(TreeNode root) {
    	//如果当前节点为空 直接返回0
        if(null == root){
            return 0;
        }
        //首先查看缓存中有没有这个节点的rob方法返回值
        if(null != cache.get(root)){
            return cache.get(root);
        }
        //计算当前节点左孩子的rob方法返回值
        int maxLeft = rob(root.left);
        //计算当前节点右孩子的rob方法返回值
        int maxRight = rob(root.right);
        int maxLeftLeft = 0;
        int maxLeftRight = 0;
        //如果当前节点有左孩子
        if(null != root.left){
        	//计算其左孩子的左孩子的rob值
            maxLeftLeft = rob(root.left.left);
            //计算其左孩子的右孩子的rob值
            maxLeftRight = rob(root.left.right);
        }
        int maxRightLeft = 0;
        int maxRightRight = 0;
        //如果当前节点有右孩子
        if(null != root.right){
        	//计算其右孩子的左孩子的rob值
            maxRightLeft = rob(root.right.left);
            //计算其右孩子的右孩子的rob值
            maxRightRight = rob(root.right.right);
        }
        //不偷当前节点能偷到的财物的最大值
        int notIncludeCurrentNodeMax = maxLeft + maxRight;
        //偷当前节点能偷到的财物的最大值
        int includeCurrentNodeMax = maxLeftLeft + maxLeftRight + maxRightLeft + maxRightRight + root.val;
        //以其中的较大值作为当前节点的rob方法返回值
        int res = notIncludeCurrentNodeMax > includeCurrentNodeMax ? notIncludeCurrentNodeMax : includeCurrentNodeMax;
        //缓存当前节点的rob方法返回值
        cache.put(root, res);
        return res;
    }
}

面经中出现过的二叉树题：

已整理

• 一、给定二叉树的先序跟后序遍历，能不能将二叉树重建（不能，因为先序：父节点-左节点-右节点，后序：左节点-右节点-父节点，两者的拓扑序列是一样的，所以无法建立），如果给出一个二叉搜索树的后续能不能建立（可以，因为只要将遍历结果排序就可以得到中序结果）。
• 二、判断一棵树是否是另一棵的子树。
• 三、 翻转二叉树
• 四、二叉树打印路径
• 六、输入一颗二叉树和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。二叉树路径和等于某个值的所有路径输出。
• 七、排序二叉树转双向链表
• 十、输入根节点和两个子节点，找到最小公共父节点，2叉树只有孩子节点；查找二叉树某两个节点的最近公共祖先
• 十二、输入二叉树节点 P, 找到二叉树中序遍历 P 的下一个节点。
• 十四、把二叉树打印成多行；中序遍历二叉树，利用O(1)空间统计遍历的每个节点的层次
• 十五、手写S型遍历二叉树，如何优化，最后说了个空间优化的方法
• 十九、leetcode 124 二叉树最大路径和

未整理

求完全二叉树的节点个数，要求最优解法，我写的是递归，复杂度O(logn*logn)