数据结构与算法题解（6）：重点掌握

最基础的数据结构与算法java实现。3

一、排序

排序面试题：

实现快速排序以及时空复杂度分析
实现归并排序以及时空复杂度分析
实现堆排序以及时空复杂度分析

1.1 归并排序

归并排序是典型的二路合并排序，将原始数据集分成两部分(不一定能够均分)，分别对它们进行排序，然后将排序后的子数据集进行合并，典型的分治法策略。

public class MergeSortTest {  
    public static void main(String[] args) {  
        int[] data = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };  
        print(data);  
        mergesort(data);  
        System.out.println("排序后的数组：");  
        print(data);  
    }
    public static void mergesort(int[] arr){
        sort(arr, 0, arr.length-1);
    }
    private static void sort(int[] a, int left, int right){
        //当left==right的时，已经不需要再划分了
        if (left<right){
            int middle = (left+right)/2;
            sort(a, left, middle);          //左子数组
            sort(a, middle+1, right);       //右子数组
            merge(a, left, middle, right);    //合并两个子数组
        }
    }
    // 合并两个有序子序列 arr[left, ..., middle] 和 arr[middle+1, ..., right]。temp是辅助数组。
    private static void merge(int arr[], int left, int middle, int right){
        int[] temp = new int[right - left + 1];
        int i=left;     
        int j=middle+1;
        int k=0;
        //将记录由小到大地放进temp数组
        while ( i<=middle && j<=right){
            if (arr[i] <=arr[j]){
                temp[k++] = arr[i++];
            }
            else{
                temp[k++] = arr[j++];
            }
        }
        while (i <=middle){
            temp[k++] = arr[i++];
        }
        while ( j<=right){
            temp[k++] = arr[j++];
        }
        //把数据复制回原数组
        for (i=0; i<k; ++i){
            arr[left+i] = temp[i];
        }
    }
    public static void print(int[] data) {  
        for (int i = 0; i < data.length; i++) {  
            System.out.print(data[i] + "\t");  
        }  
        System.out.println();  
    }
}

在合并数组的时候需要一个temp数组。我们当然有足够的理由在每次调用的时候重新new一个数组（例如，减少一个参数），但是，注意到多次的创建数组对象会造成额外的开销，我们可以在开始就创建一个足够大的数组（等于原数组长度就行），以后都使用这个数组。实际上，上面的代码就是这么写的。

时间复杂度：在归并排序中，进行一趟归并需要的关键字比较次数和数据元素移动次数最多为$n$，需要归并的趟数$log n$，故归并排序的时间复杂度为$O(nlog n)$。并且由于归并算法是固定的，不受输入数据影响，所以它在最好、最坏、平均情况下表现几乎相同，均为$O(log n)$。

空间复杂度：归并排序需要长度等于序列长度为$n$的辅助存储单元，故归并排序的空间复杂度为$O(n)$。归并排序最大的缺陷在于其空间复杂度。可不可以省略这个数组呢？不行!如果取消辅助数组而又要保证原来的数组中数据不被覆盖，那就必须要在数组中花费大量时间来移动数据。不仅容易出错，还降低了效率。因此这个辅助空间是少不掉的。
稳定性：因为我们在遇到相等的数据的时候必然是按顺序“抄写”到辅助数组上的，所以，归并排序是稳定的排序算法。

1.2 快速排序

快速排序是图灵奖得主C.R.A Hoare于1960年提出的一种划分交换排序。它采用了一种分治的策略，通常称其为分治法（Divide-and-Conquer Method）

分治法的基本思想是：将原问题分解为若干个规模更小但结构与原问题相似的子问题。递归地解这些子问题，然后将这些子问题组合为原问题的解。

利用分治法可将快速排序分为三步：

从数列中挑出一个元素作为“基准”（pivot）。
分区过程，将比基准数大的放到右边，小于或等于它的数都放到左边。这个操作称为“分区操作”，分区操作结束后，基准元素所处的位置就是最终排序后它的位置
再对“基准”左右两边的子集不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

public class quickSortTest {  
    public static void main(String[] args) {  
        int[] data = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };  
        print(data);  
        quickSort(data);  
        System.out.println("排序后的数组：");  
        print(data);  
    }
    public static void quickSort(int[] arr){
        qsort(arr, 0, arr.length-1);
    }
    private static void qsort(int[] arr, int left, int right){
        if (left < right){
            int pivot=partition(arr, left, right);        //将数组分为两部分
            qsort(arr, left, pivot-1);                   //递归排序左子数组
            qsort(arr, pivot+1, right);                  //递归排序右子数组
        }
    }
    private static int partition(int[] arr, int left, int right){
        int pivot = arr[left];     //基准记录
        while (left<right){
            while (left<right && arr[right]>=pivot) --right;
            arr[left]=arr[right];             //交换比基准小的记录到左端
            while (left<right && arr[left]<=pivot) ++left;
            arr[right] = arr[left];           //交换比基准大的记录到右端
        }
        //扫描完成，基准到位
        arr[left] = pivot;
        //返回的是基准的位置
        return left;
    }
        public static void print(int[] data) {  
        for (int i = 0; i < data.length; i++) {  
            System.out.print(data[i] + "\t");  
        }  
        System.out.println();  
    }
}

二、查找

2.1 二分查找

int binary_search(int array[],int n,int value)    
{    
    int left=0;    
    int right=n-1;    
    while (left<=right)  
    {    
        int middle=left + ((right-left)>>1);      
        if (array[middle]>value)    
        {    
            right =middle-1;   //right赋值，适时而变    
        }     
        else if(array[middle]<value)    
        {    
            left=middle+1;    
        }    
        else    
            return middle;          
    }    
    return -1;    
}

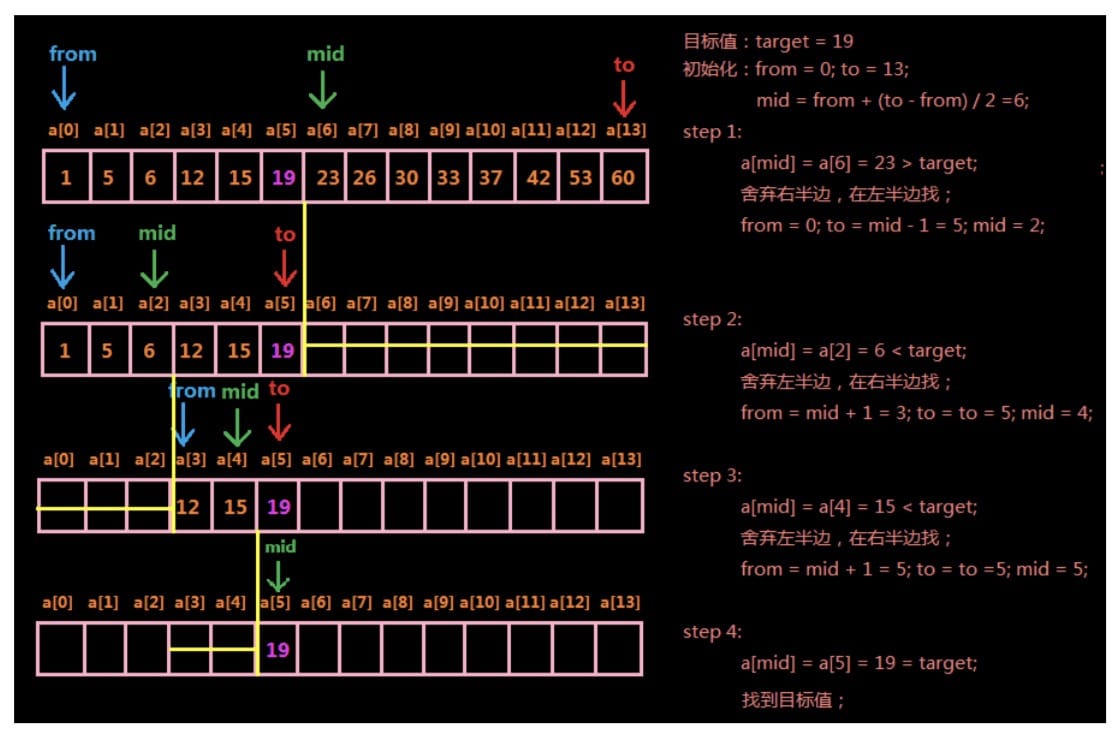
三、二叉树

这块内容讨论二叉树的常见遍历方式的代码（java）实现，包括前序（preorder）、中序（inorder）、后序（postorder）、层序（levelorder），进一步考虑递归和非递归的实现方式。

递归的实现方法相对简单，但由于递归的执行方式每次都会产生一个新的方法调用栈，如果递归层级较深，会造成较大的内存开销，相比之下，非递归的方式则可以避免这个问题。递归遍历容易实现，非递归则没那么简单，非递归调用本质上是通过维护一个栈，模拟递归调用的方法调用栈的行为。

在此之前，先简单定义节点的数据结构：

二叉树节点最多只有两个儿子，并保存一个节点的值，为了实验的方便，假定它为 int。同时，我们直接使用 Java 的 System.out.print 方法来输出节点值，以显示遍历结果。

class Node{  
    public int value;  
    public Node left;  
    public Node right;  
    public Node(int v){  
        this.value=v;  
        this.left=null;  
        this.right=null;  
    }  
      
}

3.1 前序遍历

3.1.1 递归实现

递归实现很简单，在每次访问到某个节点时，先输出节点值，然后再依次递归的对左儿子、右儿子调用遍历的方法。代码如下

java

public void preOrder(Node root){
    if(root!=null){
        System.out.print(root.value);
        preOrder(root.left);
        preOrder(root.right);
    }
}

3.1.2 非递归实现

利用栈实现循环先序遍历二叉树，维护一个栈，将根节点入栈，只要栈不为空，出栈并访问，接着依次将访问节点的右节点、左节点入栈。这种方式是对先序遍历的一种特殊实现，简洁明了，但是不具备很好地扩展性，在中序和后序方式中不适用。

public void preOrder(Node root){
    if(root==null)return;
    Stack<Node> stack = new Stack<Node>();
    stack.push(root);
    while(!stack.isEmpty){
        Node temp = stack.pop();
        System.out.print(temp.value);
        if(temp.right!=null)stack.push(temp.right);
        if(temp.left!=null)stack.push(temp.left);
    }
}

还有一种方式就是利用栈模拟递归过程实现循环先序遍历二叉树。这种方式具备扩展性，它模拟了递归的过程，将左子树不断的压入栈，直到null，然后处理栈顶节点的右子树。

java

public void preOrder(Node root){
    if(root==null)return;
    Stack<Node> s = new Stack<Node>();
    while(root!=null||!s.isEmtpy()){
        while(root!=null){
            System.out.print(root.value);、//先访问
            s.push(root);//再入栈
            root = root.left;
        }
        root = s.pop();
        root = root.right;//如果是null，出栈并处理右子树
    }
}

3.2 中序遍历

3.2.1 递归实现

public void inOrder(Node root){
    if(root!=null){
        preOrder(root.left);
        System.out.print(root.value);
        preOrder(root.right);
    }
}

3.2.2 非递归实现

利用栈模拟递归过程实现循环中序遍历二叉树。跟前序遍历的非递归实现方法二很类似。唯一的不同是访问当前节点的时机：前序遍历在入栈前访问，而中序遍历在出栈后访问。

java

public void inOrder(Node root){
    if(root==null)return;
    Stack<Node> s = Stack<Node>();
    while(root!=null||s.isEmpty()){
        while(root!=null){
            s.push(root);
            root=root.left;
        }
        root = s.pop(root);
        System.out.print(root.value);
        root = root.right;
    }
}

3.3 后序遍历

3.3.1 递归实现

public void inOrder(Node root){
    if(root!=null){
        preOrder(root.left);
        preOrder(root.right);
        System.out.print(root.value);
    }
}

3.3.2 非递归实现

public void postOrder(Node root){
    if(root==null)return;
    Stack<Node> s1 = new Stack<Node>();
    Stack<Node> s2 = new Stack<Node>();
    Node node = root;
    s1.push(node);
    while(s1!=null){//这个while循环的功能是找出后序遍历的逆序，存在s2里面
        node = s1.pop();
        if(node.left!=null) s1.push(node.left);
        if(node.right!=null)s1.push(node.right);
        s2.push(node);     
    }
    while(s2!=null){//将s2中的元素出栈，即为后序遍历次序
        node = s2.pop();
        System.out.print(node.value);
    }
}

3.4 层序遍历

public static void levelTravel(Node root){  
        if(root==null)return;  
        Queue<Node> q=new LinkedList<Node>();  
        q.add(root);  
        while(!q.isEmpty()){  
            Node temp =  q.poll();  
            System.out.println(temp.value);  
            if(temp.left!=null)q.add(temp.left);  
            if(temp.right!=null)q.add(temp.right);  
        }  
    }