在竞价广告中,广告主能否获得某个广告位是由其变现能力也就是eCPM的大小来决定的。在以CPC结算即点击结算的单子中,eCPM即千次展示期望收入的计算公式为:其中:
- $\mu$ 表示点击率(click rate),是由供给方在媒体侧通过收集广告数据(a)、用户数据(u)、上下文数据(c),使用模型预估用户在当前环境下,对当前广告的点击概率
- $v$ 表示点击价值(click value),是由需求方根据用户在广告主自身站内的行为数据评估出来的一个出价
但需求方往往不会完全按照其估计的真实点击价值来定价,而往往会以较低的价格寻求套利空间,为了避免这种套利行为,就有了竞价广告的定价策略,通过机制设计来抑制广告主积极调价。这也是本文所关注的。
假如我们有一组广告,记为集合A,另有一组广告位,记为集合S,那么一次广告竞价过程可以描述为:集合A中的广告通过出价来拍卖集合B中的广告位置,拍卖的依据是广告的eCPM。其中出价是很重要的一环,所以其机制设计就尤为重要,要做到竞价市场收益良好,稳定且公平。
从拍卖理论说起
广告位置竞价源自于拍卖理论,看具体的拍卖方式之前先说一个概念,帕累托有效,即拍卖品最终归于支付意愿最高的竞买人之手,支付意愿并不由出价呈现,而是一种买家的心理状态。拍卖方式主要有四种,英国式拍卖、荷兰式拍卖、第一价格密封拍卖、第二价格密封拍卖,如下:
英国式拍卖:
- 也叫增价拍卖,指拍卖竞价由低向高依次递增,直到以最高价击槌成交的一种拍卖,拍卖人设定一个保留价格,如果最终的出价低于保留价,则流拍。为了保证竞价收敛,一般会为竞价设定一个终止时间。
- 英式拍卖最古老,也是大家接触较多的拍卖方式。在这种拍卖方式中,竞买人要冒一定的风险,他可能会被令人兴奋的竞价过程吸引,出价超出了预估价,这种心理现象称为“赢者诅咒”。
荷兰式拍卖:
- 与英国式拍卖相反,也称减价拍卖,它是指拍卖竞价由高到低依次递减,直到第一个竞买人应价时击槌成交的一种拍卖。它起源于荷兰的鲜花交易市场,拍卖周期很短,所以对于短期易腐食品,如果蔬、鱼类、鲜花较为适合。
- 它克服了英式拍卖中“知道其他买家出价”的缺点,是一种密封式的拍卖方法。竞买人往往坐等观望,企盼价格不断减低,因而现场竞争气氛不够热烈。所以有“无声拍卖”的名声。
第一价格密封拍卖:
- 每一个买方写下自己的期望价格,买方之间互不知道对方的出价(故称密封拍卖),最后在同一个时间揭晓每个买家的出价,出价最高者获得标的物。
- 这种拍卖方式每个买家只出一次价格,一般来讲,买方会出一个低于心理预期的价格,只有在买方足够多的情况下,最终的价格才会更接近物品的真实价值;且由于存在一些暗箱操作,无法真的保证密封性。
第二价格密封拍卖:
- 也叫维克里拍卖(Vickrey Auction),拍卖过程和第一价格密封拍卖一致,由出价最高的买家获得物品,但他只需要支付所有投标者中的第二高价。在维克里拍卖中,每个买家最优出价策略就是“自己对这个物品价格的估值”,即“诚实才是最优的竞价策略”,因为这种策略的最后的成交价格和买家的出价是相对独立的,中标者对价格没有影响,出标的高低只决定最后是否获得标的,但不决定最终的成交价格。比如竞标一幅画,最终中标人出价是2万元,未中标人中最高价格是1.8万元,所以中标人只需要出1.8万元。
- 在这种策略下,买家可以将所有精力放到对物品价值的评估上,而不需要研究其他竞争对手,不需要研究投标策略,不需要进行市场评估。理论上讲,第二价格密封拍卖是一种有效的拍卖机制。但实际中,买家之间合谋,买家与卖家之间合谋的情况经常存在;同时,作为非理性人,其他买家的出价在一定程度上也会影响自己的出价。
维克里拍卖是诺贝尔经济学奖获得者维克里的名字命名的。他在《反投机、拍卖与竞争性密封投标》文中对拍卖理论做了非常开创性的工作,首次运用博弈论来分析拍卖问题, 极富预见性地提出了拍卖理论中的多数关键问题, 从而引导了该理论的基本研究方向。这也是他在1996年获得诺贝尔经济学家奖的重要因素。他在论文中主要证明了以下几个结论:
- 英式拍卖中的每个竞买人的占优战略都是保持竞价, 直到价格达到自己的估价为止, 估价最高的竞买人将以大致等于次高估价的价格夺走拍卖品, 这种配置结果显然是帕累托有效的。
- 在竞买人对称的荷式拍卖中, 每个竞买人的报价应该严格低于自己的估价, 估价最高的竞买人也必定成为赢家, 因而也是帕累托有效的。但是, 如果竞买人非对称, 荷式拍卖的配置结果很可能是无效率的。
- 荷式拍卖与第一价格密封拍卖在战略上是完全等价的, 因为竞买人在两种情形中所面临的局势完全相同。在此基础上,维克里独创性地提出了英式拍卖的密封等价形式第二价格密封拍卖,即维克里拍卖。这种拍卖最显著的特征是每个竞买人的的占优战略都是按其真实支付意愿出价(说真话), 这种拍卖机制显然是激励相容的。由于拍卖品最终归于支付意愿最高的竞买人之手, 它也是一种具有帕累托效率的配置机制。
- 维克里最重要的贡献在于, 他针对竞买人对称的情形证明, 荷式拍卖与英式拍卖所产生的期望价格相同。结合战略等价关系, 这实际上意味着四种标准拍卖机制给卖主带来的平均收入相等。这就是著名的收入等价定理,该定理是整个拍卖理论研究的起点。
具体的可以研读阅读论文《反投机、拍卖与竞争性密封投标》或者Vijay Krishna的《Auction Theory》了解更多的拍卖理论的细节。互联网广告中常用的的二价定价策略就是从维克多拍卖推广开来的,具体看一下。
广义第二高价
广义第二高价(GSP)是互联网广告中运用最广泛的定价方式,像谷歌、百度运用的都是该策略。其原理如下:
单位置第二高价拍卖
- 和拍卖理论中的维克里拍卖一致,指的是在只有一个位置的拍卖中,向赢得该位置的广告主收取其下一位广告主的出价,比如说耐克出10块,阿迪出8块,那么耐克赢得单广告位展示,但最终的定价是8元。
多位置广义第二高价拍卖
- 由单位置二价拍卖推广开来放到搜索广告的多广告位拍卖中,对赢得每一个位置的广告主,都按照他下一位的广告位置出价来收取费用。
如果最终的单子按照CPM即曝光收费,广义第二高价拍卖可直接应用;
如果是按照CPC即点击结算,广告主出价是根据点击来的,而竞价是根据eCPM排序的,最终的定价需要进行如下的换算:
也就是根据以下一位的广告位置的eCPM作为分子,以该位置的点击率加上一个很小的$\Delta$作为分母,两者相除得到该位置的定价,具体的计算可以看最后的定价示例。
VCG定价
VCG 定价是 Vickrey、Clarke 和 Groves 在研究竞价系统均衡状态时得到的一种理论上较为优越的定价策略。
其基本思想是:对于赢得了某个位置的广告主,其所付出的成本应该等于他占据这个位置给其他市场参与者带来的价值损害。有点类似于机会成本的概念。
在这一原则下,VCG的定价策略可以表示为公式:
其优点是:
- 在VCG定价策略的稳定状态下,每个广告主都找到了自己的最优状态
- 相较于其他定价策略,VCG向广告主收取的费用最少
但VCG并不主流,只有少数的广告厂商如facebook使用,其缺陷如下:
- 定价逻辑过于复杂,很难向广告主解释清
- “给其他市场参与者带来的价值损害”的计算很难验证
市场保留价
和拍卖过程一直,互联网竞价市场也会设置一个拍卖底价,即市场保留价(Market Reserve Price,MRP),也称底价或起价。这个底价体现在两个方面:
- 出价只有在高于底价时才有竞价机会
- 若赢得了广告位,根据定价策略计算出的费用低于市场保留价,也需要调整到底价的水平
如何确定底价:
- 竞争较为充分时、广告主深度足够时,底价可以设的高一些
- 反之则适当降低
底价的设置方式:
- 整个竞价市场采用同样的保留价格
- 根据不同的标的物设置不同的保留价格,一般对竞争激烈的关键词设置较高的MRP,这个也叫动态市场保留价
底价的基本原理
- 根据竞价广告主的eCPM分布,找到一个使得填充率没有明显下降的CPM底价,然年后再根据质量度倒算其CPC底价。
动态市场保留价
- 雅虎搜索关键词动态调价,即对不同的关键词调整不同的起价,对收入的影响达到13%,谷歌也更早推出其动态调价策略
- 动态调价与a/u/c都有关,可以做到完全的动态,具体可参考文献Reserve Prices in Internet Advertising Auctions:A Field Experiment∗
价格挤压
在CPC广告竞价机制设计中,会对eCPM的计算公式 $eCPM = \mu * bid_{CPC}$做一些微调,如下:
其中k大于0,k越大,对出价的挤压就越大,故称价格挤压因子。看两种极端情况:
- $k\rightarrow \infty$:只根据点击率排序,不考虑出价的作用
- $k\rightarrow 0$:只根据出价排序
作用:根据市场情况更主动影响竞价体系朝着需要的方向发展
- 若市场上存在大量的出价较高但品质不佳的广告主,则可调高$k$来强调质量和用户反馈的影响,即更多的体现点击率;同时想鼓励广告主提高广告质量和相关性,也可以提高$k$
- 若市场竞价激烈程度不足,可降低$k$鼓励竞争,并短期增加营收
定价示例与算法实现
目前主流的定价体系综合运用了以上所述的GSP、市场保留价和价格挤压三种策略,下面是一个具体示例:
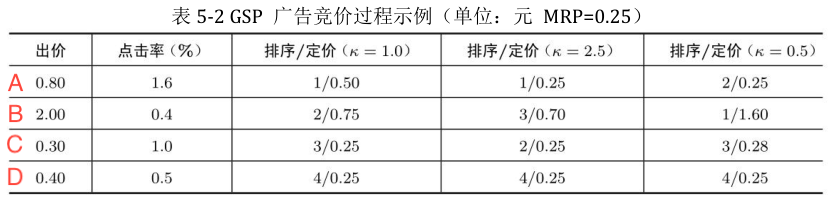
A/B/C/D四个广告竞价,其中底价MRP为0.25元,第一列为广告主出价,第二列为预估的点击率,第三、四、五列分别是$k=1.0/2.5/0.5$时的eCPM排序和最终定价,以第三列为例说一下计算的步骤:
1、对每一个广告按照给定的挤压因子计算调整后的eCPM
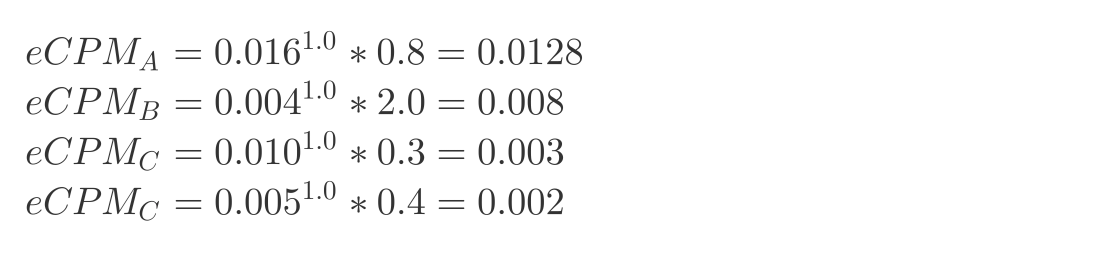
所以其eCPM排序为 $A:1,B:2,C:3,D:4$
2、依据GSP策略计算定价,此处$\Delta$设为0
A的下一排序是B,所以$q_s = \frac{eCPM_B}{\mu_s}= 0.008/0.016 = 0.5$
B的下一排序是C:所以$q_s = \frac{eCPM_C}{\mu_s}= 0.003/0.004 = 0.75$
C的下一排序是D:所以$q_s = \frac{eCPM_D}{\mu_s}= 0.002/0.01 = 0.2$,因为底价MRP=0.25,故最终的定价为0.25
D为最后一个广告,没有下一排序广告,所以按照底价定价为0.25
整个计算过程比较简单,下面用python实现一下GSP定价的过程。
|
|
参考资料:
定价问题延伸阅读:
- Research Frontier of Real-Time Bidding based Display Advertising
- Budget Constrained Bidding by Model-free Reinforcement Learning in Display Advertising
- Real-Time Bidding with Multi-Agent Reinforcement Learning in Display Advertising
- Real-Time Bidding by Reinforcement Learning in Display Advertising
- Combining Powers of Two Predictors in Optimizing Real-Time Bidding Strategy under Constrained Budget
- Bid-aware Gradient Descent for Unbiased Learning with Censored Data in Display Advertising
- Optimized Cost per Click in Taobao Display Advertising
- Real-Time Bidding Algorithms for Performance-Based Display Ad Allocation
- Deep Reinforcement Learning for Sponsored Search Real-time Bidding

