所谓决策,就是在几个方案中选择一个方案,分为风险决策和非风险决策。在非风险决策中,各个方案的结果都是确定的。在风险决策中,有的方案有的结果是不确定的,即可能发生,也可能不发生。我们这里谈及的就是风险决策。
一般来说,风险决策研究有两个途径:
- 一个是规范性途径,其基本问题是:人类的风险决策应该遵循怎样的规则?
- 一个是描述性途径,其基本问题是:人类的风险决策实际遵循怎样的规则?
规范性途径往往被叫做决策逻辑学,描述性途径往往被叫做决策行为学或决策心理学。我们这里关注的是描述性途径。
关于风险决策的最早理论是期望效用理论,它最初只是规范性理论,但经济学家们逐渐把它当做描述性理论来使用——把它作为经济学中对人的决策行为的基本假定,即认为人的实际决策行为遵循期望效应理论,直到上世纪70年代处有的著名经济学家(如Arrow)仍然采取这种做法。
自1979年以来,Kahneman & Tversky的一系列著作,对期望效用理论作为描述性理论的有效性提出了严峻的挑战,并提出前景理论作为合适的描述理论。由于前景理论能够精确解释、预言许多风险决策行为,它的影响越来越大;后来Kahneman把它应用于经济学领域,对经济学产生了深远的影响,为此,Kahneman于2002年获得了诺贝尔经济学奖。
这里首先介绍期望效用理论;然后介绍Kahneman等以实验事实对期望效用理论作为描述性理论的批评;最后介绍前景理论的主要内容。
一、期望效用理论
期望效用函数理论是20世纪50年代,冯·纽曼和摩根斯坦(von Neumann and Morgenstem)在公理化假设的基础上,运用逻辑和数学工具,建立了不确定条件下对理性人(rational actor)选择进行分析的框架。不过,该理论是将个体与群体合而为一的。后来,阿罗和德布鲁(Arrow and Debreu)将其吸收进瓦尔拉斯均衡的框架中,成为处理不确定决策问题的分析范式,进而构建起现代微观经济学并由此展开的包括宏观、金融、计量等在内的宏伟而又优美的理论大厦。
期望效用理论本来是作为规范性理论提出的,但后来在许多经济学著作中被应用为描述性理论,直到上个世纪70年代初仍然如此。
经济学上所使用的期望效用理论包括三方面的内容:Bayes框架;Savage公理;Bernoulli原则。它们分别由不同的人在不同的时期创建。以下分述之。
1.1 Bayes框架
早在1662年,Antoine Arnauld就写道:决定一个人必须做什么以获得好处或避免坏处,不仅必须考虑好处和坏处本身,而且必须考虑它发生或不发生的概率。
大约在100年之后出版的Bayes的遗著(1763)年把这个思想系统化、精确化,形成了所谓的风险决策的Bayes框架,其核心思想可以概括为两点:
- $ED(A_i)=\sum _jP_{ij}·D_{ij}$:即行动$A_i$的估计渴望度(estimated desirability,简称ED;后来改称期望效用,expected utility,EU)等于它的各个可能结果的渴望度$D_{ij}$乘以该可能结果出现的概率所得的积的和;或者说,行动$A_i$的估计渴望度等于它的各个结果的渴望度的加权和,权重为各个结果的概率。(注意,前提是各个可能结果互不相容。)
- 根据贝叶斯原则进行选择:选择有着最大估计渴望度的一个方案。
请注意到Bayes决策框架所包含的两点假设:
- 决策权重=概率本身
- 渴望度(效用)不依赖于参考点。Bayes决策框架并没有要求以一个参考点来衡量渴望度(效用);实际上,在经济学中人们往往以财富的最终状态来计算效用。
1.2 Savage公理
Bayes决策框架一直沿用下来,并有进一步的发展。
Von Neumann & Morgenstern(1944)发展出关于偏好(选择)的公理系统;而Ramsey(1931)和Savage(1954)继续发展了该公理系统,用主观概率代替客观概率,从而使概率理论和决策理论可以适用于更广泛的事情。Savage公理系统是这些公理系统中最为成熟的。其中的公理有:
- 不变性公理(Invariance Axiom):方案间的偏好顺序不依赖于方案的描述方式。
- 优势性公理(Dominance Axiom):如果方案A在每个方面至少跟方案B一样好,而在至少一个方面比B更好,那么A应该比B更可取。
- 如果方案B由于方案A,那么它们与任一概率$p≠0$的结合所得的$(B,p)$一定优于$(A,p)$
这些公理与直觉十分一致;也与Bayes决策框架完全一致。
1.3 Bernoulli原则
很早以前Bernoulli就指出人们通常是风险回避的。一个决策是风险回避的,是指:按照结果的表面值(如金额)计算,在确定的结果与有着相等或更高的期望值的不确定的结果之间,决策者选择了确定的结果,如,A. 确定得到80元;B.81%的可能得到100元,按结果的表面值计算,B的期望值高于A,按理应该选择B,但事实上大多数人们会选择A。
为了解释这个现象,Bernoulli提出:人们评价方案,不是用方案的金钱结果值,而是用这些金钱结果值的主观价值,而这个主观价值对于金钱值的函数曲线(效用曲线)是一条凹形的曲线,即$u’’(x)<0$。通俗地说,随着x的不断增大,u的增长越来越慢。用这个原理能轻易解释上段提及的现象。假设80元的主观价值是72,由此可以推出100元的主观价值应该小于90(因为前面80元中每20元的主观价值是18,根据u增长越来越慢的原理,100元超出80元的那20元的主观价值应该小于18,因而100元的主观价值小于90),假设是85.于是,A方案的期望值是72,而B的期望值是$85*81%=68.85$。所以大多数人们选择了A方案。
于是,风险回避和$u’’(x)<0$也成了一些经济学著作对人的决策行为的假定之一。
1.4 小结与问题
经济学理论中常常把期望效用理论的上述Bayes框架,Savage公理和Bernoulli原则中的全部或部分作为对人的风险决策行为的基本假定,在此假定和其他假定的基础上构建经济学理论。
这种做法有明显的方法论问题:这些经验假定(经验命题)的真假并没有经过经验方法的系统判明。逻辑学家们提出Bayes框架,Savage公理的初衷是:高斯人们应该怎样决策,或者说怎样决策才是合乎理性的;他们并未考察人们的决策行为是否恰好符合这些规则。而Bernoulli原则知识根据某类风险决策事实归纳得出;并未建立在对各种类型的风险决策事实的全面考察上。人们的实际决策行为是否遵循上述规则,显然是个经验命题;而一个经验命题只有通过经验的方法才能判明它的真伪。而经济学家们,未经经验方法的判定,就把上述规则当做经验命题来使用,这种做法就存在方法论上的问题。
这种方法论上的问题使得采用期望效用理论作为描述性理论可能是错误的。而Kahneman & Tversky的一系列实验表明:采用期望效用理论作为描述性理论确实是错误的。
二、对期望效用理论的实验挑战
Kahneman & Tversky的一系列实验对期望效用理论作为描述理论的有效性提出了挑战。下面是他们的部分实验。
2.1 实验一
期望效用理论的“决策权重=概率”成立吗?
问题一:
请选择:
- A. 有80%的可能性得到4000元; 【20%】
- B. 确定地得到3000元。【80%】
方括号指的是该项被试的百分比,以下皆同。
问题二:
请选择:
- C. 有20%的可能性得到4000元;【65%】
- D. 有25%的可能性得到3000元。【35%】
分析:
如前1.1 所述,期望效用理论中,决策权重=概率。假设这点成立,那么有:
注意到$U(A),U(B)$分别乘以0.25就相应得到$U(C),U(D)$,所以有:
如果$U(A)
但上述实验结果却是:虽然在A、B之间大部分偏好B;但在C、D之间大部分偏好C。即在集体水平上被试的偏好发生了逆转。另外,根据Kahneman & Tversky的实验报告,在个体水平上,超过半数的被试的偏好也发生了逆转。
实验结果与假设推论相矛盾。可见,期望效用理论中的“决策权重=概率”这一假定并不符合人的真实的决策行为。
另外,由于C就是25%概率的A,D就是25% 的B,按照期望效用理论的替代性公理,A、B之间的偏好关系,与C、D之间的偏好关系相同,实验结果却是偏好发生了逆转。可见,期望效用理论的替代性公理在人们的实际行为中也不成立。
2.2 实验二
期望效用理论的不变性公理成立吗?
下面是许多人都熟知的一个实验,但也许并非大家都知道其理论蕴涵。
问题一:想象有一场流行病,预计将杀死600人。有两个预防方案,你希望哪个方案被征服采纳?
- 如果A方案被采纳,200人将被挽救; 【72%】
- 如果B方案被采纳,有 1/3 的可能性 600 人都被挽救,有 2/3 的可能性没有人能得到挽救。 【28%】
问题二:
- 如果方案 C 被采纳,400 人将死亡; 【22%】
- 如果方案 D 被采纳,有 1/3 的可能性没有人死亡并且有 2/3 的可能性 600 人都会死亡。 【78%】
分析
期望效用理论的不变性公理认为:人们的选择不因描述方式不同而改变。 假设这点成立,那么,因为方案 A 等价于方案 C,而 B 等价于 D,所以 A,B 之间的偏好顺序与 C,D 之间的偏 好顺序应该是一样的。但事实上它们是相反的。假设有误。这说明人的决策行为并不遵循期望效用理论的不变性公理。
另外,上述偏好逆转发生的原因在于:在问题 1 中,被试被诱导把 600 人都会死作为参 考点,从而把问题表征为确定的 200 人被挽救与 1/3 可能的 600 人被挽救之比较;而在问题 2 中,被试被诱导把 0 人死亡作为参考点,从而把问题表征为确定的 400 人死亡与 2/3 可能 的 600 人死亡。问题表征上的这种不同进而导致了决策上的不同。由此我们看到:决策中, 人们并非以财富数值或生命个数的最终状态来计算主观价值,而是根据财富数值或生命个数 相对于参考点的值来计算主观价值。这也违反了期望效用理论。
2.3 实验三
期望效用理论的优势性公理成立吗?
问题一:
请选择
- E.有25%的机会获得240元并有75%的机会失去760元; 【0%】
- F. 有 25%的机会获得 250 元并有 75%的机会失去 750 元 。【100%】
问题二:
假想你面临两组选择。请先仔细阅读两组选择,然后作出选择:
第一组选择:
- A. 固定得到 240 元【84%】
- B. 25%的机会得到 1000 元,75%的机会得到 0 元。【16%】
第二组选择:
- C.固定失去 750 元;【13%】
- D.75%的机会失去 1000 元,25%的机会失去 0 元 【87%】
分析:
期望效用理论的优势性公理认为:如果方案 A 在每个方面至少跟方案 B 一样好,而在至少一个方面比 B 更好,那么 A 应该比 B 更可取。假设这点成立,那么,由于 A 优于 B, D 优于 C,那么,A+D 应该优于 B+C;而注意到 A+D=E, B+C=F;所 以,E 应该优于 F。但事实相反,所有的被试都认为 F 优于 E。可见,人们的决策行为并不 遵循期望效用理论的优势性公理。
2.4 实验四
期望效用理论的“风险回避”原则总是成立吗?
问题一:
请选择:
- A. 确定得到 1 元;
- B. 1%的可能性得到 100 元,99%的可能性得到 0 元。
人们大多会选择 B.
问题二:
- C.确定失去 90 元;
- D.有 90%的可能性失去 100 元,有 10%的可能性失去 0 元。
人们大多会选择 D.
分析
经济学家所用的期望效用理论的“风险回避”原则认为:在按表面结果 值计算有着相等期望值的风险选项与确定选项之间,人们往往会选择确定项而回避风险项。但在上面这些决策问题上,大多数人们风险寻求,而非风险回避。可见期望效用理论的 “风险回避”原则在人们的实际决策行为中并不总是成立。
事实上,Kahneman 和 Tversky 的研究发现人们的风险态度有如下的模式:
| 中、大概率 | 小概率 | |
|---|---|---|
| 得 | 风险回避 | 风险寻求 |
| 失 | 风险寻求 | 风险回避 |
三、Kahneman和Tversky的前景理论
上述实验事实表明:人们的风险决策行为系统地偏离了期望效用理论。那么人们的风险决策行为究竟遵循怎样的规律呢?Kahneman和Tversky提出了前景理论(prospect theory)作为上述问题的答案。
前景理论的核心内容是:价值函数(曲线)与权重函数(曲线)。
3.1 价值函数(曲线)
价值函数把表面价值如金额转化为决策价值,其具体形式是:
其中x是表面价值如金额的得失,得为正,失为负;v为决策价值。在Kahneman & Tversky的一个研究中,被试者们的中位参数$\alpha = \beta =0.88;\gamma = 2.25$;其他研究者也得到了相近的数值。
其曲线如下图所示: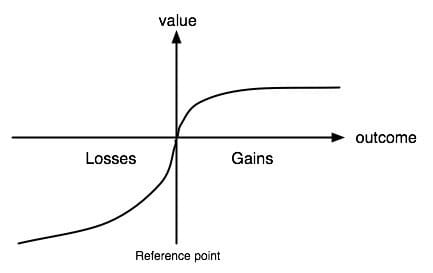
它有如下特点:
- 其定义域不是财富,而是财富的变化、得失,即财富相对于某个参考点的差距,这个参考点往往是当前的财富状态。
- 整个函数是个递增函数;$v(0) = 0$
- 在得(Gains)的区域呈凹形,在失(LOSSES)的区域呈凸形(即当$x>0$时,$v’’(x)<0$;当$x<0$时,$v''(x)>0$)。用通俗的话来说就是,随着$|x|$的不断增大,$v$的变化越来越小。例如,从0元到10元所引起的价值上的变化,要大于从100元到110元所引起的价值上的变化。
- 在失的区域的曲线比在得的区域的曲线更加陡峭。通俗地说,失去100元所带来的痛苦的程度要大于100元所带来的快乐的程度。
3.2 权重函数(曲线)
权重函数把概率转化为决策权重。当风险前景为两个结果时,其具体的形式如下: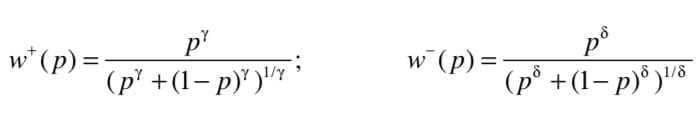
其中,p为概率,$w^+(p)$为得到时的决策权重,$w^-(p)$为失去时的决策权重。在Kahneman的一个实验中,求得被试们的中位参数$\lambda = 0.61,\delta =0.69$。其他研究者也得到相近的结果。
其曲线如下图所示: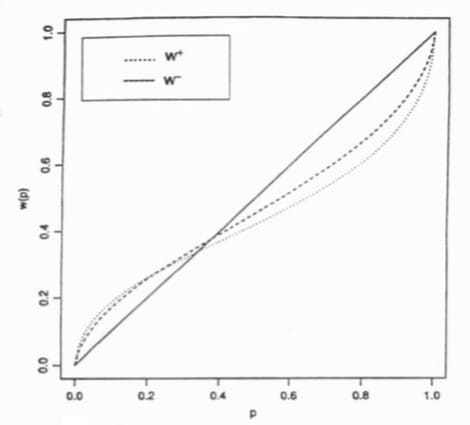
- 其中的$w^+$为得到时的权重,$w^-$为失去时的权重。当概率较小时,同等概率下,$w^+$大于$w^-$;当概率中等或较大时,同等概率下,$w^+$小于$w^-$
无论$w^+$还是$w^-$都有以下特点:
- $w(0)=0$;$w(1)=1$;$w$是$p$的递增函数。
- 给予小概率以过高的权重(注意,并非高估小概率,因为被试清除地直到概率是多少;只是小概率所对应的权重高于高于概率本身)
- 给予中、高概率以较小的权重,即低于概率自身的权重。
- 次确定性:$w(p)+w(1-p)<1$,其中$0<p<1$
- 次比例性:$\frac{w(pq)}{w(p)}≤\frac{w(pqr)}{w(pr)}$
- 次可加性,包括:
- 下端次可加性:$w(p+q)≤w(p)+w(q)$,其中$p+q<1$
- 上端次可加性:$w(1)-w(1-p)≥w(p+q)-w(q)$,其中$p≠0$
计算各个前景的价值,比较并作出选择。应用$v(x)$函数和$w(p)$函数,就能求出各个结果的$v$值和$w$值;把这些$v$值和$w$值代入$V$公式,就能求出各个前景的V值:
其中V为一个前景的心理价值;$w_i$和$v(x_i)$分别是第i个结果的决策权重和决策价值;结果分得失即正负,所以结果的下标也分正负。然后比较各个前景的V值,选出最高V值的前景
以上就是前景理论所描述的人们的决策行为规律。
用上述规律,不仅能够轻易而一致地解释前面提到的各种违背期望效用理论的实验现象;还能很好地解释和预言大量的其他实验现象。Kahneman后来把这个理论应用于经济学领域,对经济学的微观基础产生了巨大的影响,为此,Kahneman获得了2002年的诺贝尔经济学奖。
四、通俗解释
在《赌客信条》一书中,作者孙惟微将前景理论归纳为5句话:
- “二鸟在林,不如一鸟在手”,在确定的收益和“赌一把”之间,多数人会选择确定的好处。所谓“见好就收,落袋为安。称之为“确定效应”。
- 在确定的损失和“赌一把”之间,做一个抉择,多数人会选择“赌一把”。称之为“反射效应”。
- 白捡的100元所带来的快乐,难以抵消丢失100元所带来的痛苦。称之为“损失规避”。
- 很多人都买过彩票,虽然赢钱可能微乎其微,你的钱99.99%的可能支持福利事业和体育事业了,可还是有人心存侥幸搏小概率事件。称之为“迷恋小概率事件”。
- 多数人对得失的判断往往根据参照点决定,举例来说,在“其他人一年挣6万元你年收入7万元”和“其他人年收入为9万元你一年收入8万”的选择题中,大部分人会选择前者。称之为“参照依赖”。
4.1 确定效用
所谓确定效应(certainty effect),就是在确定的好处(收益)和“赌一把”之间,做一个抉择,多数人会选择确定的好处。用一个词形容就是“见好就收”,用一句话打比方就是“二鸟在林,不如一鸟在手”,正所谓落袋为安。
让我们来做这样一个实验。
- A.你一定能赚30000元。
- B.你有80%可能赚40000元,20%可能性什么也得不到。
你会选择哪一个呢?实验结果是,大部分人都选择A。
传统经济学中的“理性人”这时会跳出来批判:选择A是错的,因为40000×80%=32000,期望值要大于30000。这个实验结果是对“原理1”的印证:大多数人处于收益状态时,往往小心翼翼、厌恶风险、喜欢见好就收,害怕失去已有的利润。卡尼曼和特韦斯基称为“确定效应”(certainty effect),即处于收益状态时,大部分人都是风险厌恶者。
“确定效应”表现在投资上就是投资者有强烈的获利了结倾向,喜欢将正在赚钱的股票卖出。投资时,多数人的表现是“赔则拖,赢必走”。在股市中,普遍有一种“卖出效应”,也就是投资者卖出获利的股票的意向,要远远大于卖出亏损股票的意向。这与“对则持,错即改”的投资核心理念背道而驰。
4.2 反射效应
面对两种损害,你是会选择躲避呢,还是勇往直前?当一个人在面对两种都损失的抉择时,会激起他的冒险精神。在确定的坏处(损失)和“赌一把”之间,做一个抉择,多数人会选择“赌一把”,这叫“反射效应”。用一句话概括就是“两害相权取其轻”。
让我们来做这样一个实验。
- A.你一定会赔30000元。
- B.你有80%可能赔40000元,20%可能不赔钱。
你会选择哪一个呢?投票结果是,只有少数人情愿“花钱消灾”选择A,大部分人愿意和命运抗一抗,选择B。
传统经济学中的“理性人”会跳出来说,两害相权取其轻,所以选B是错的,因为(-40000)×80%=-32000,风险要大于-30000元。现实是,多数人处于亏损状态时,会极不甘心,宁愿承受更大的风险来赌一把。也就是说,处于损失预期时,大多数人变得甘冒风险。卡尼曼和特韦斯基称为“反射效应”(reflectioneffect)。
“反射效应”是非理性的,表现在股市上就是喜欢将赔钱的股票继续持有下去。统计数据证实,投资者持有亏损股票的时间远长于持有获利股票。投资者长期持有的股票多数是不愿意“割肉”而留下的“套牢”股票。
4.3 损失规避
如何理解“损失规避”?用一句话打比方,就是“白捡的100元所带来的快乐,难以抵消丢失100元所带来的痛苦”。前景理论最重要也是最有用的发现之一是:当我们做有关收益和有关损失的决策时表现出的不对称性。对此,就连传统经济学的坚定捍卫者 保罗·萨缪尔森,也不得不承认:“增加100元收入所带来的效用,小于失去100元所带来的效用。”
这其实是前景理论的第3个原理,即“损失规避”(loss aversion):大多数人对损失和获得的敏感程度不对称,面对损失的痛苦感要大大超过面对获得的快乐感。
行为经济学家通过一个赌局验证了这一论断。
假设有这样一个赌博游戏,投一枚均匀的硬币,正面为赢,反面为输。如果赢了可以获得50000元,输了失去50000元。请问你是否愿意赌一把?请做出你的选择。
- A.愿意
- B.不愿意
从整体上来说,这个赌局输赢的可能性相同,就是说这个游戏的结果期望值为零,是绝对公平的赌局。你会选择参与这个赌局吗?但大量类似实验的结果证明,多数人不愿意玩这个游戏。为什么人们会做出这样的选择呢?这个现象同样可以用损失规避效应解释,虽然出现正反面的概率是相同的,但是人们对“失”比对“得”敏感。想到可能会输掉50000元,这种不舒服的程度超过了想到有同样可能赢来50000元的快乐。由于人们对损失要比对相同数量的收益敏感得多,因此即使股票账户有涨有跌,人们也会更加频繁地为每日的损失而痛苦,最终将股票抛掉。一般人因为这种“损失规避”(loss aversion),会放弃本可以获利的投资。
4.4 迷恋小概率事件
买彩票是赌自己会走运,买保险是赌自己会倒霉。这是两种很少发生的事件,但人们却十分热衷。前景理论还揭示了一个奇特现象,即人类具有强调小概率事件的倾向。
何谓小概率事件?就是几乎不可能发生的事件。如天上掉馅饼,这就是个小概率事件。掉的是馅饼固然好,但如果掉下来的不是馅饼而是陷阱呢?当然也属于小概率事件。
面对小概率的赢利,多数人是风险喜好者。面对小概率的损失,多数人是风险厌恶者。
事实上,很多人都买过彩票,虽然赢钱可能微乎其微,你的钱99.99%的可能支持福利事业和体育事业了,可还是有人心存侥幸搏小概率事件。
同时,很多人都买过保险,虽然倒霉的概率非常小,可还是想规避这个风险。人们的这种倾向,是保险公司经营下去的心理学基础。
在小概率事件面前人类对风险的态度是矛盾的,一个人可以是风险喜好者,同时又是风险厌恶者。传统经济学无法解释这个现象。
小概率事件的另一个名字叫运气。侥幸,就是企求好运,邀天之幸。孔子很反感这种事,他说:“小人行险以侥幸。”庄子认为孔子是个“灯下黑”,他借盗跖之口评价孔子:“妄作孝弟,而侥幸于封侯富贵者也。”对小概率事件的迷恋,连圣人也不能免俗。
前景理论指出,在风险和收益面前,人的“心是偏的”。在涉及收益时,我们是风险的厌恶者,但涉及损失时,我们却是风险喜好者。但涉及小概率事件时,风险偏好又会发生离奇的转变。所以,人们并不是风险厌恶者,他们在他们认为合适的情况下非常乐意赌一把。归根结底,人们真正憎恨的是损失,而不是风险。
这种损失厌恶而不是风险厌恶的情形,在股市中常常见到。比如,我们持有一只股票,在高点没有抛出,然后一路下跌,进入了彻彻底底的下降通道,这时的明智之举应是抛出该股票,而交易费用与预期的损失相比,是微不足道的。
扪心自问,如果现在持有现金,还会不会买这只股票?你很可能不会再买吧,那为什么不能卖掉它买别的更好的股票呢?也许,卖了它后损失就成了“事实”吧。
4.5 参照依赖
假设你面对这样一个选择:在商品和服务价格相同的情况下,你有两种选择:
- A.其他同事一年挣6万元的情况下,你的年收入7万元。
- B.其他同事年收入为9万元的情况下,你一年有8万元进账。
卡尼曼的这调查结果出人意料:大部分人选择了前者。事实上,我们拼命赚钱的动力,多是来自同侪间的嫉妒和攀比。我们对得与失的判断,是来自比较。嫉妒总是来自自我与别人的比较,培根曾言:皇帝通常不会被人嫉妒,除非对方也是皇帝。对此,美国作家门肯早有妙论:“只要比你小姨子的丈夫(连襟)一年多赚1000块,你就算是有钱人了。”
传统经济学认为金钱的效用是绝对的,行为经济学则告诉我们,金钱的效用是相对的。这就是财富与幸福之间的悖论。到底什么是“得”,什么是“失”呢?你今年收入20万元,该高兴还是失落呢?假如你的奋斗目标是10万元,你也许会感到愉快;假如目标是100万元,你会不会有点失落呢?所谓的损失和获得,一定是相对于参照点而言的。卡尼曼称为“参照依赖”(Reference Dependence)。
老张最幸福的时候是他在20世纪80年代做“万元户”的时候,虽然现在自己的村镇已经改造成了城市,拆迁补贴也让自己成为了“百万元户”,但他感觉没有当年兴奋,因为邻里都是“百万元户”了。
讲这个故事的用意不难明白,我们就不再进行烦琐的论证了 得与失都是比较出来的结果。传统经济学的偏好理论(Preference theory)假设,人的选择与参照点无关。行为经济学则证实,人们的偏好会受到单独评判、联合评判、交替对比及语意效应等因素的影响。
参照依赖理论:多数人对得失的判断往往根据参照点决定。一般人对一个决策结果的评价,是通过计算该结果相对于某一参照点的变化而完成的。人们看的不是最终的结果,而是看最终结果与参照点之间的差额。一样东西可以说成是“得”,也可以说成是“失”,这取决于参照点的不同。非理性的得失感受会对我们的决策产生影响。
综上,前景理论引申出五个基本结论
- 确定效应:处于收益状态时,多数人是风险厌恶者。
- 反射效应:处于损失状态时,多数人是风险喜好者。
- 迷恋小概率事件:面对小概率的赢利,多数人是风险喜好者;面对小概率的损失,多数人是风险厌恶者。
- 损失规避:多数人对损失比对收益敏感。
- 参照依赖:多数人对得失的判断往往由参照点决定。
简言之,人在面临获利时,不愿冒风险;而在面临损失时,人人都成了冒险家。而损失和获利是相对于参照点而言的,改变评价事物时的参照点,就会改变对风险的态度。

